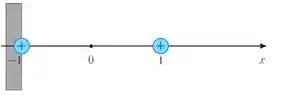
Considere duas cargas elétricas com carga unitária e positiva, fixadas num eixo perpendicular a uma parede, como na figura abaixo. O potencial elétrico gerado por essas duas partículas num ponto ao longo desse eixo é dado, em unidades convenientes, pela

seguinte função

(a) Verifique que o potencial elétrico é dado por

(b) Calcule a força exercida numa partícula de carga unitária posicionada em , dada

por .

(c) Calcule os pontos críticos de e determine seus extremos locais e seus intervalos

de crescimento e decrescimento. A força se anula em algum ponto?

(d) Determine os pontos de inflexão de e seus intervalos de concavidade para cima

e para baixo.

(e) Determine as assíntotas verticais e horizontais de e esboce seu gráfico.

Primeiramente, para resolver a alternativa vamos precisar analisar os dois conjuntos de função:

Se você perceber bem, no primeiro caso você tem uma representação de uma soma de duas frações, já no segundo caso não.

Observando isso vamos primeiramente tirar o MMC para unificar as somas, logo:

Agora vamos analisar conforme o domínio, podemos ver que não pode ser e nem . Porque quando colocamos esses valores, nosso potencial tem uma indeterminação indo para infinito.

Portanto, vamos realizar a análise primeiramente com . Analisando nesse intervalo, temos que:

Substituindo na fórmula acima, temos que:

Quando temos que geramos as seguintes igualdades:

Sendo assim temos que:

Confirmando a igualdade.

Para calcular os pontos críticos, vamos precisar da derivada de primeira ordem do potencial, e para o cálculo da força também iremos precisar.

Porque do enunciado, temos que . Sendo assim, derivando a expressão vamos responder a alternativa e .

Vamos encontrar a derivada do potencial que está no intervalo .

Para resolver vamos utilizar a regra do quociente das derivadas, logo:

Agora vamos realizar a mesma operação para calcular a força ao longo do intervalo

Aplicando a regra do quociente:

Logo, temos que a força é:

Como temos que os pontos críticos são os pontos na qual a força se anula, sendo assim:

Como condição de continuidade, o denominador não pode ser . Logo temos que:

Da primeira equação tiramos que é ponto crítico, na segunda equação temos que não existe real.

Analisando ainda a força temos que

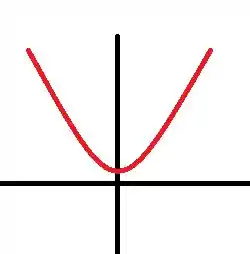
Logo, só precisamos analisar o numerador que é . Sendo assim, no intervalo a derivada é negativa, logo o potencial é decrescente, consequentemente temos que a derivada é positiva gerando uma função crescente.

Como temos o seguinte perfil da função: A função é decrescente até o e depois se torna crescente até o , gerando o seguinte gráfico:

Normalmente para resolver alternativa iriamos precisar da seguinte equação:

Porém, temos que existe apenas o ponto crítico e identificamos a característica do gráfico antes, podemos concluir que é um ponto de mínimo.

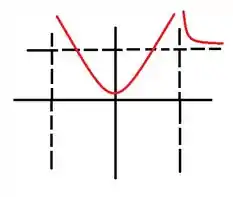
Para resolver a última alternativa iremos utilizar o conceito de assíntotas de cálculo 1. Na prática, é entender o que acontece com a função quando se aproxima das indeterminações e quando as funções tendem ao infinito.

Como vamos tender ao infinito. Temos que , portanto:

Sendo assim, temos que é uma assíntota horizontal.

Agora vamos analisar as descontinuidades que é e , porém aqui temos uma região de descontinuidade. Logo precisamos analisar os limites laterais.

Vamos começar tendendo a pela direita, logo os valores de é tudo maior do que . Portanto:

Agora vamos realizar a mesma análise com tendendo a tanto pela esquerda, quanto pela direita.

Tendendo a pela esquerda temos que os valores de é menor do que , sendo assim:

Agora fazendo tender a pela direita os valores de é tudo maior do que . Sendo assim, temos que:

Sendo assim, nosso gráfico é algo do tipo: