Lista de Aplicações Cálculo 1 - UnB de Cálculo 1 da UnB - Lista 10

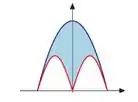
Considere a função definida por , divida o intervalo em partes iguais como o indicado na figura abaixo e resolva os itens a seguir.

Defina, para cada , o ponto e calcule .

Defina agora e calcule

Usando a seguinte formula:

Lembrando que a integral e o limite, quando , do somatório em (1), encontre a área delimitada pelo gráfico da função e o eixo .

Seja uma função contínua. Considere e os valores máximo e mínimo de em , respectivamente.

1. Use as propriedades da integral para verificar que:
2. Usando o Teorema do Valor Intermediário, conclua que existe tal que
3. Usando o mesmo raciocínio mostre que, se é uma função não negativa tal que , então existe tal que:

Seja uma função contínua e defina:

1. Para e pequeno, use as propriedades da integral e o Teorema da

Média para verificar que

para algum .

2. Usando o item anterior e a continuidade de f, mostre que
3. Repita o argumento acima para , e conclua que a função e derivável e
4. Supondo agora que é uma primitiva qualquer de f, mostre que

Suponha que, no instante , a posição em relação à origem de uma partícula que se desloca ao longo de uma reta seja dada por em que é a função velocidade, cujo gráfico está ilustrado abaixo. Considere ainda que seja dado em segundos, que seja dada em metros e que, para , o gráfico de seja um segmento de reta. A partir do gráfico da função velocidade, julgue os itens a seguir.

1. A partícula está se afastando da origem entre os instantes .
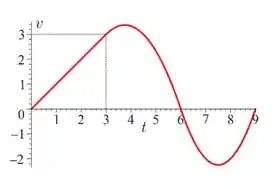
2. A partícula percorre menos de metros nos primeiros segundos.
3. No instante a partícula está na origem.
4. No instante a posição da partícula é positiva.
5. O espaço total percorrido pela partícula igual a

A figura ao lado indica a área delimitada pelos gráficos das funções

E

Com . Use a integral definida para calcular o valor dessa área.