Lista de Aplicações Cálculo 1 - UnB de Cálculo 1 da UnB - Lista 8

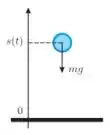
4) Para uma bola arremessada verticalmente sem resistência do ar, temos que a energia mecânica

Se conserva, onde e são, respectivamente, a posição e a velocidade instantâneas, é a massa do bloco e é a gravidade. Supondo que , e que , temos que é a solução da seguinte equação

Como ilustra os itens a seguir, a equação pode ser melhor entendida a partir do fato de que, se a derivada de uma função for identicamente nula em um intervalo, então a função é necessariamente constante.

a) Calcule as derivadas das funções e .

b) Lembrando que se uma função tem derivada identicamente nula em um intervalo , então ela é constante em , use o item anterior e as informações dadas para obter uma relação entre as funções e .

c) Use o item anterior e a condição inicial para obter a expressão de .

d) Determine a velocidade no instante .

5) Denote por a velocidade de um corpo de massa que foi lançado verticalmente com velocidade inicial e sujeito a uma força de resistência do ar . Nesse caso, usando a aproximação da aceleração da gravidade, pode-se mostrar que é solução do problema de valor inicial

Para encontrar a solução , resolva os itens seguintes.

a) Calcule as derivadas das funções e .

b) Lembrando que se uma função tem derivada identicamente nula em um intervalo , então ela é constante em , use o item anterior e as informações dadas para obter uma relação entre as funções e .

c) Use o item anterior e a condição inicial para obter a expressão de .

d) Determine o instante em que o corpo alcança a altura máxima.