UFPE – Física 1 – 1ºEE – 2019.2 – Questão 6
Uma partícula executa um movimento circular uniforme (MCU) no plano , com centro na origem e sentido anti-horário. Em certo instante o seu vetor velocidade (em m/s) vale . No instante , o vetor posição da partícula é , onde R é o raio do MCU.
Sabendo que o período do MCU é , qual é a sua aceleração centrípeta (em ) no instante ?
Passo 1
Vamos lá! Precisamos lembrar que o módulo da aceleração centrípeta é
Como ele nos diz que o movimento é circular uniforme, podemos concluir que o módulo da velocidade será sempre o mesmo. Sendo assim,
Passo 2
Como nenhuma das alternativas nos fornecem uma resposta em função de , precisamos descobrir de onde sai aquele .
Lembra que
Sabendo que a distância percorrida em um período é
Logo
Então o módulo da aceleração centrípeta é
Passo 3
Agora precisamos identificar a direção e o sentido.
Sabendo que em a partícula está na posição é e que quando a partícula retorna para a posição de , podemos dizer que em a partícula está na metade do caminho. Lembrando que a aceleração centrípeta é orienta para o centro, podemos esboçar o esquema no desenho a seguir.
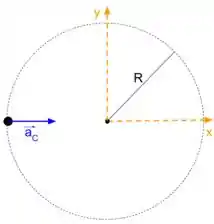
Assim podemos escrever que
Sendo assim, a alternativa correspondente é a letra (a).