Um bloco de massa encontra-se inicialmente mantido em repouso sobre um plano inclinado de um ângulo , preso a uma das pontas de uma corda ideal (veja a Figura 2). A corda passa por uma polia ideal e tem a sua outra ponta presa a um bloco de massa . Os coeficientes de atrito estático e cinético entre e o plano inclinado são e , respectivamente. Considere , e . Num certo instante, o conjunto dos blocos é liberado.
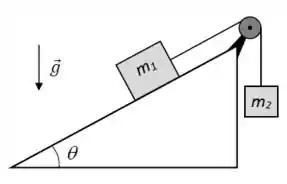
- Faça o diagrama de corpo livre de cada bloco depois que o conjunto é liberado, desenhando e nomeando todas as forças que atuam sobre eles.
- Calcule o módulo da força normal que o plano inclinado exerce sobre .
- Depois de liberado, o conjunto se move? Justifique sua resposta.
- Calcule o módulo da força de tração na corda.
- Calcule o módulo da força de atrito e especifique seu sentido.
Passo 1
Vamos lá! Podemos montar o diagrama da seguinte forma
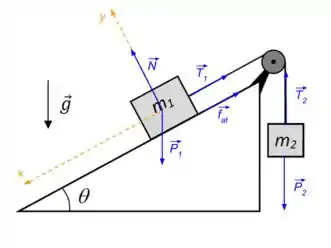
Onde é a força peso do bloco 2 e é a tração no bloco 2 aplicada pela corda, é a tração do da corda no bloco 1, é o peso do bloco 1, é a força que o plano exerce sobre o bloco 1 e é a força de atrito entre o bloco 1 e o plano.
A força de atrito está orientada subindo a rampa, pois
Com isso o bloco 1 tenderia a descer e o bloco 2 a subir.
Passo 2
Para o item (b), usando o sistema de coordenadas descritos na figura, sabendo que não há movimento no eixo para o bloco , podemos dizer que
Passo 3
Para o item (c), devemos considerar que, como
e
o bloco 1 desceria pelo plano. Portanto, a força de atrito seria no sentido . Então para que o bloco entre em movimento, precisamos saber se
Passo 4
Considerando que
Portanto, os blocos não vão se movimentar.
Passo 5
Agora vamos partir para o item (d).
Como já calculamos acima, a tração na corda é
Passo 6
Agora só falta o item (e).
Como vimos acima, os blocos não vão se movimentar. Sendo assim, podemos escrever que para o bloco 1, temos
Pronto. Já resolvemos tudo!