2º EE de Física 1 da UFPE - 2019.2

Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força conservativa, cuja energia potencial é mostrada na Figura 1. Inicialmente, a partícula encontra-se na posição com velocidade . Não existem forças dissipativas.

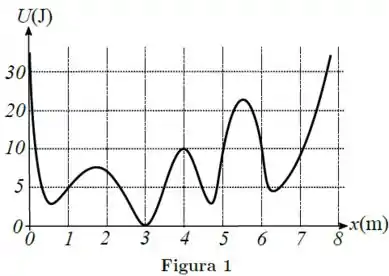
Considere as afirmativas abaixo:

(I) A força em é positiva (isto é, no sentido positivo do eixo ).

(II) O trabalho realizado pela força entre e é positivo.

(III) A variação da energia mecânica entre e é negativa.

Marque a alternativa que contém apenas afirrmativa(s) verdadeira(s).

(a) I

(b) II

(c) III

(d) I e II

(e) I e III

(f) II e III

(g) Todas

(h) Nenhuma

Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força conservativa, cuja energia potencial é mostrada na Figura 1. Inicialmente, a partícula encontra-se na posição com velocidade . Não existem forças dissipativas.

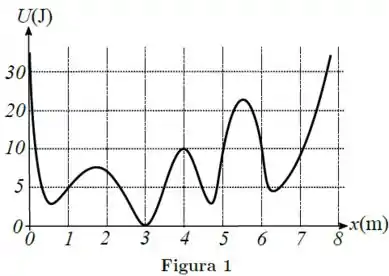
Ao passar pela posição , a velocidade da partícula é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Um projétil de massa incide com velocidade inicial sobre um alvo de massa , inicialmente parado sobre uma superfície horizontal sem atrito. O alvo tem forma curva na área atingida pelo projétil, conforme mostra a Figura 2. Ao perder o contato com o alvo, o projétil possui velocidade . Devido ao contato com o projétil, o alvo passa a se mover horizontalmente para a direita. Despreze os efeitos da gravidade sobre o movimento do projétil.

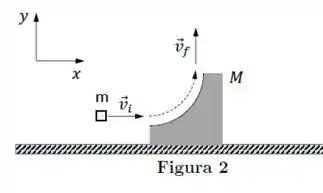
Seja a velocidadedo alvo no instante final em que ele perde contato com o projétil. A variação do momento linear do alvo entre os instantes inicial e final é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Um projétil de massa incide com velocidade inicial sobre um alvo de massa , inicialmente parado sobre uma superfície horizontal sem atrito. O alvo tem forma curva na área atingida pelo projétil, conforme mostra a Figura 2. Ao perder o contato com o alvo, o projétil possui velocidade . Devido ao contato com o projétil, o alvo passa a se mover horizontalmente para a direita. Despreze os efeitos da gravidade sobre o movimento do projétil.

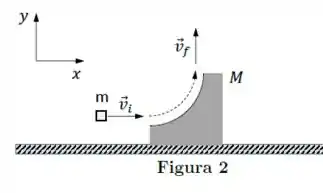
A variação do momento linear do projétil entre o instante inicial e o instante em que ele perde contato com o alvo é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

Uma partícula de massa move-se ao longo do eixo horizontal sujeita à ação de uma única força conservativa, cuja energia potencial é mostrada na Figura 1. Inicialmente, a partícula encontra-se na posição com velocidade . Não existem forças dissipativas.

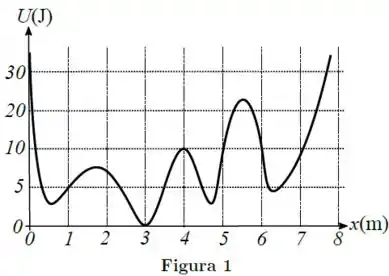
Além de um ponto de retorno no intervalo, em que a energia cinética da partícula é nula, há também um outro ponto de retorno no intervalo (em metros):

(a)

(b)

(c)

(d)

(e)

(f)

(g)

Considere que as massas do projétil e do alvo são e , respectivamente. Se o módulo da velocidade inicial do projétil é , então o módulo da velocidade do alvo no instante em que ele perde contato com o projétil é:

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Um bloco de massa encontra-se inicialmente mantido em repouso, comprimindo de uma mola de constante elástica (ver Figura 3). Quando o bloco liberado, ele perde contato com a mola antes do ponto . Não existe atrito antes do ponto .

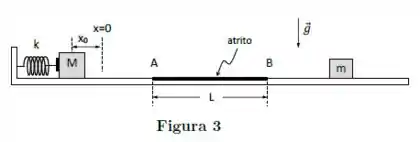
(a) Calcule a velocidade do bloco no ponto .

(b) Entre os pontos e o bloco atravessa uma região de comprimento com Coeficiente de atrito cinético . Calcule o trabalho realizado pela força de atrito nessa região. Considere .

(c) Calcule a velocidade do bloco no ponto

(d) Após o ponto , o atrito deixa de existir e o bloco realiza uma colisão perfeitamente inelástica com um outro bloco de massa que se encontrava inicialmente parado. Calcule a velocidade dos blocos após a colisão.