UFPE – Física 1 – 1ºEE – 2019.2 – Questão 1
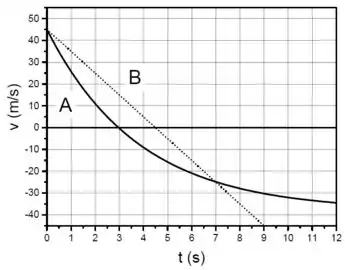
O gráfico da Figura mostra a velocidade em função do tempo de duas partículas (A e B) em movimento retilíneo.
Considere as afirmativas abaixo:
(I) A velocidade inicial (em t = 0) da partícula B é igual à velocidade inicial da partícula A.
(II) A aceleração da partícula A é igual à aceleração da partícula B no instante t = 7 s.
(III) A aceleração média da partícula A entre os instantes t = 0 e t = 7 s é maior que a aceleração média da partícula B entre os mesmos instantes.
Marque a alternativa que contém apenas afirmativa(s) verdadeira(s).
(a) I
(b) II
(c) III
(d) I e II
(e) I e III
(f) II e III
(g) Todas
(h) Nenhuma
Passo 1
Vamos lá! Precisamos verificar cada afirmativa.
Na afirmativa :Como temos um gráfico e no instante é um dos valores de onde as linhas de A e B se cruzam, podemos dizer que as velocidades são iguais. Portanto, a afirmativa está CORRETA.
Passo 2
Agora podemos verificar a afirmativa .
Se liga. Observe que no ponto a reta de B intercepta a curva de A, sendo assim, as velocidades são iguais. Logo após esse encontro, as velocidades são diferentes, portanto, a aceleração é diferente.Uma outra forma de ver, isto é, fazendo as derivadas das funções de A e B para . Portanto, a afirmativa está INCORRETA.
Passo 3
Vamos verificar a afirmativa
Aqui precisamos lembrar que
Aplicando os valores para A e B no intervalo de e , temos
Portanto, as acelerações médias de A e B no intervalo de e são iguais. Sendo assim, a afirmativa está INCORRETA.
(I) Verdadeira.
(II) Falsa.
(III) Falsa.
A alternativa correta é a letra (a).