UFPE – Física 1 – 1ºEE – 2019.2 – Questão 2
O gráfico da Figura mostra a velocidade em função do tempo de duas partículas (A e B) em movimento retilíneo.
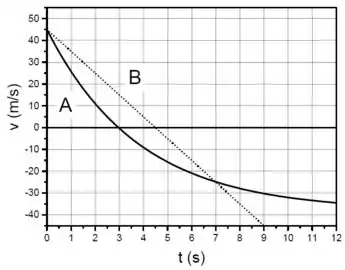
A aceleração média da partícula A entre os instantes e é:
Passo 1
Vamos lá! Precisamos calcular a aceleração média.
Lembra que
Como o intervalo desejado é entre e , basta olharmos para o gráfico.
Passo 2
Olhando para o gráfico vemos que
Agora só precisamos calcular a aceleração
Podemos ver que a resposta é a alternativa (c).
Resposta
Exercícios de Livros Relacionados
Um trenó a vela está se movendo para leste com velocidade constante quando uma rajada de vento produz uma aceleração constante para leste durante 3,0s . O gráfico de x em função de t aparece na Fig. 2
Os carros A e B se movem no mesmo sentido em pistas vizinhas. A posição x do carro A é dada na Fig.2 - 27 , do instante t = 0 ao instante t = 7,0s . A escala vertical do gráfico é definida por x s = 3
A Figura 2-13 mostra a aceleração da cabeça e do tronco de um voluntário durante urna colisão frontal. Qual é a velocidade (a) da cabeça e (b) do tronco quando a aceleração da cabeça é máxima?
Que distância percorre em 16s um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por v 1 = 8,0m .
A figura mostra um gráfico de x em função de t para um objeto se movendo ao longo de uma linha reta. Para esse movimento, esboce os gráficos (usando o mesmo eixo t ) de (a) v x como função de t , e (b