2º EE de Física 1 da UFPE - 2016.1

Preencha os campos com a sua resposta.

Uma força atua sobre uma partícula cuja trajetória é dada por:

Onde o tempo é dado em segundos.

O trabalho realizado pela forma sobre a partícula no intervalo de tempo entre e é igual a ____ , enquanto a potência aplicacda ao bloco em é igual a ____ .

Nos gráficos ao lado estão representadas possíveis trajetórias de colisão de duas partículas de mesma massa em um sistema isolado. Em cada gráfico as trajetórias são mostradas para o mesmo intervalo de tempo. As setas indicam o sentido do movimento em cada trajetória. Quais dos gráficos são compatíveis com trajetórias das partículas antes e depois de uma colisão?

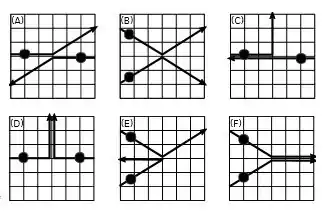
(a) A, B, C, D

(b) B, C, D

(c) A, B, D, E

(d) A, E, F

(e) B, C, F

(f) A, B, F

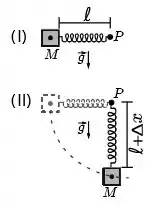
Uma mola de constante elástica tem uma de suas extremidades fixas em um ponto e um corpo de massa preso à outra extremidade. A mola tem comprimento de repouso , massa desprezível e pode girar sem atrito em torno do ponto . Em um dado instante [figura (I)] o sistema massa-mola se encontra na posição horizontal com a mola indeformada, sendo, então, liberado a partir do repouso. Ao passar pela posição mostrada na figura (II) sabe-se que a distância do corpo de massa ao ponto é igual a . A aceleração gravitacional no local tem módulo . Assinale a alternativa correta quanto ao módulo da velocidade do corpo na posição da figura (II).

(a)

(b)

(c)

(d)

(e)

(f)

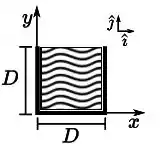
A figura ao lado mostra um sistema formado por três hastes retilíneas, cada uma de comprimento e massa , conectadas em forma de e uma chapa quadrada (região hachurada), de aresta e massa . Considere que as espessuras das hastes e da chapa são iguais e muito menores do que . Assinale a alternativa que corretamente expressa a posição do centro de massa do sistema (hastes + chapa):

(a)

(b)

(c)

(d)

(e)

(f)

Um bloco de massa é lançado, a partir do repouso, ao longo de uma rampa sem atrito de um ponto situado a uma altura do plano horizontal, como esquematizado na figura abaixo. Ao final da rampa, o bloco colide com o bloco de massa , inicialmente em repouso próximo ao ponto . A colisão é completamente inelástica. Após o ponto há um trecho da pista horizontal (região hachurada na figura a partir do ponto ) cujo coeficiente de atrito cinético é . Considere .

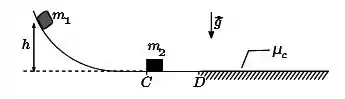
(a) Calcule o módulo da velocidade do bloco imediatamente antes da colisão.

(b) Determine as velocidades dos blocos imediatamente após a colisão. Baseado em qual princ´ıpio de conservação é possível encontrar esse resultado?

(c) Ao percorrer o trecho com atrito os blocos inevitavelmente param. Calcule a distncia percorrida pelos blocos nesse trecho a partir do ponto até que fiquem em repouso.

(d) Calcule a razão entre o trabalho realizado pela força de atrito sobre os blocos até que fiquem em repouso e a energia cinética inicial perdida durante a colisão .

Uma partícula de massa pode se deslocar ao longo do eixo horizontal, orientado positivamente para a direita (vide figura). Sobre ela atua uma única força conservativa e variável , cuja energia potencial associada está representada na figura abaixo. Inicialmente, a partícula encontra-se em com velocidade .

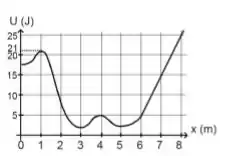
(a) Calcule a velocidade da partícula em .

(b) Qual é o trabalho realizado pela força entre e ? Justifique sua resposta.

(c) Quando a partícula passa por , a força é para a esquerda ou para a direita? Calcule o módulo da força nessa posição.