Uma partícula de massa pode se deslocar ao longo do eixo horizontal, orientado positivamente para a direita (vide figura). Sobre ela atua uma única força conservativa e variável , cuja energia potencial associada está representada na figura abaixo. Inicialmente, a partícula encontra-se em com velocidade .
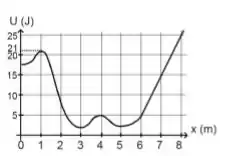
(a) Calcule a velocidade da partícula em .
(b) Qual é o trabalho realizado pela força entre e ? Justifique sua resposta.
(c) Quando a partícula passa por , a força é para a esquerda ou para a direita? Calcule o módulo da força nessa posição.
Passo 1
(a) Da soma das energias potencial e cinética em determinanos a energia mecânica do sistema,
A velocidade da partícula em , , é obtido da conservação da energia mecânica do sistema,
Passo 2
(b) A variação da energia potencial, , associada a uma força conservativa é definida como menos o trabalho realizado por esta força, . Portanto, o trabalho realizado pela força entre e , , é dado por
Passo 3
Como e em , então e o sentido desta força é para a esquerda. O módulo dessa força pode ser obtido do fato de entre e ser uma reta. Logo,
Resposta
(a)
(b)
(c)