Um bloco de massa é lançado, a partir do repouso, ao longo de uma rampa sem atrito de um ponto situado a uma altura do plano horizontal, como esquematizado na figura abaixo. Ao final da rampa, o bloco colide com o bloco de massa , inicialmente em repouso próximo ao ponto . A colisão é completamente inelástica. Após o ponto há um trecho da pista horizontal (região hachurada na figura a partir do ponto ) cujo coeficiente de atrito cinético é . Considere .

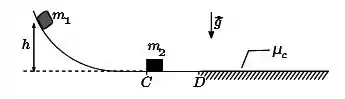
(a) Calcule o módulo da velocidade do bloco imediatamente antes da colisão.

(b) Determine as velocidades dos blocos imediatamente após a colisão. Baseado em qual princ´ıpio de conservação é possível encontrar esse resultado?

(c) Ao percorrer o trecho com atrito os blocos inevitavelmente param. Calcule a distncia percorrida pelos blocos nesse trecho a partir do ponto até que fiquem em repouso.

(d) Calcule a razão entre o trabalho realizado pela força de atrito sobre os blocos até que fiquem em repouso e a energia cinética inicial perdida durante a colisão .

(b) Da conservação do momento linear em uma colisão obtemos:

onde e são as velocidades imediatamente após a colisão. Como a colisão é unidimensional e completamente inelástica (onde velocidade do centro de massa do sistema e após a colisão) então:

(c) Os blocos percorrem a mesma distância até parar. Esta distância pode ser calculada a partir do teorema trabalho – energia cinética. Denotando como a força de atrito cinético sobre os blocos, então:

(d) Temos que: