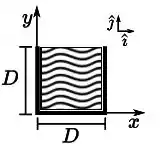
A figura ao lado mostra um sistema formado por três hastes retilíneas, cada uma de comprimento e massa , conectadas em forma de e uma chapa quadrada (região hachurada), de aresta e massa . Considere que as espessuras das hastes e da chapa são iguais e muito menores do que . Assinale a alternativa que corretamente expressa a posição do centro de massa do sistema (hastes + chapa):
(a)
(b)
(c)
(d)
(e)
(f)
Passo 1
Os centros de massa de cada haste se encontra no meio delas, portanto, podemos encontrar o centro de massa do conjunto de hastes da seguinte maneira:
Já para a coordenada :
Passo 2
O centro de massa da chapa é fácil de saber, já que ela é quadrada e homogênea:
Passo 3
Para encontrar o centro de massa do sistema, basta fazermos que:
E para a coordenada :
Portanto:
Resposta
(b)