Física 1 UFPE 2ºEE 2019.1
Uma partícula de massa m = 2,0 kg move-se ao longo do eixo x sujeita a uma única força F. A dependência de F com a posição x da partícula é mostrada na Figura 1. A energia potencial associada à forçaa F é U. Quando a partícula está em x = 0, ela tem velocidade = 2,0 m/s no sentido positivo do eixo x.
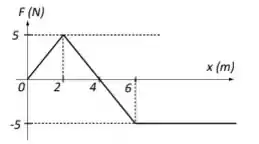
Em qual posição a partícula para momentaneamente antes de retornar?
a) 2,0 m
b) 2,8 m
c) 3,8 m
d) 4,0 m
e) 5,8 m
f) 6,0 m
g) 7,0 m
h) 7,8 m
i) 8,0 m
Passo 1
Como já sabemos:
E pela conservação de Energia Mecânica, sabemos que a partícula vai parar quando a Energia Potencial é Máxima. Nos pontos máximos e mínimos, a derivada de uma função deve ser 0. Então, para os pontos máximos de U, a derivada de F deve ser 0. Como o sinal é invertido, o ponto onde a energia cinética é mínima é o ponto onde F é máximo, ou seja, em x=2m.
Resposta
a) 2,0m