Duas massas de modelar deslizam sobre uma superfície horizontal de gelo, sem atrito. As massas possuem velocidades iniciais , e colidem de forma que seguem juntas com velocidade , conforme a Figura abaixo.
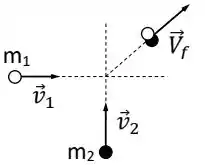
A variação da energia cinética total das massas, , devido a colisão é:
a) 0 J
b) −6,0 J
c) −3,0 J
d) −1,5 J
e) 1,5 J
f) 3,0 J
g) 6,0 J
h) 8,0 J
Passo 1
Como a gente já calculou a velocidade final do sistema e temos a velocidade de cada uma das partículas, temos que:
Então:
Substituindo todos valores, temos que:
Pronto! Conseguimos!
Resposta
b) −6,0 J