Na Figura 3, o bloco A de massa = 2,0 kg encontra-se inicialmente em repouso, preso a uma mola ideal comprimida de 0,10 m. A constante el ́astica da mola vale k = 40 N/m. Nos itens a seguir, considere g = e despreze todos os atritos. O bloco não perde o contato com a superfície.
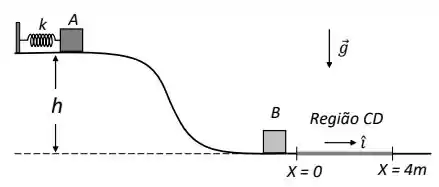
a) Calcule a velocidade do bloco ap ́os descer a rampa de altura h = 0,19 m em relação ao nível do solo.
b) Após descer a rampa, o bloco A sofre uma colisão perfeitamente inelástica com um bloco B de massa = 8,0 kg inicialmente em repouso. A colisão faz um bloco grudar no outro. Calcule a velocidade dos blocos imediatamente após a colisão.
c) Após a colisão, os blocos permanecem grudados e ingressam na região CD horizontal, com início na posição x = 0 e término em x = 4,0 m. Nessa região, os blocos estão sujeitos a força variável (em newtons), que os acelera para a frente, onde x é a posição dos blocos e é o vetor unitrio horizontal para a direita. Calcule o trabalho realizado por F entre as posições x = 0 e x = 4,0 m.
Sugestão: Faça o gráfico de F em função de x.
Passo 1
Pela comservação de Energia Mecânica, temos que:
Onde
Pronto! Como no começo o bloco tá em repouso, Energia Cinética inicial será 0. E no final, teremos apenas Energia Cinética, pois não teremos altura nem uma mola agindo no nosso corpo, então temos:
Isolando nossa velocidade final, ficamos com:
Agora, substituindo os valores que a questão nos deu e passando tudo pra metros, temos que:
Passo 2
Como n ̃ao h ́a for ̧cas externas atuando sobre as massa no momento da colisão, o momento total é conservado:
Portanto, temos que:
Como é 0, substituindo todos os outros dados da questão, temos que:
Passo 3
Na região CD a forçaa vari ́avel na direção de x positivo é F(x) = 0,5 · x de modo que o trabalho realizado por esta força no intervalo desejado é:
Outra forma de calcular esse trabalho de uma força variável pode ser calculando a área do gráfico da força pela distância. Que teríamos algo assim:
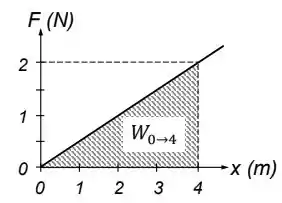
Onde chegaríamos ao mesmo resultado calculando a área do triângulo hachurado.