P1 de Física 1 da UFRJ - 2014.1

Um projétil é lançado do solo com uma velocidade que faz um ângulo com a horizontal . Ignorando efeitos de resistência do ar e considerando o intervalo de tempo decorrido entre o instante do lançamento e o instante em que o projétil volta a altura em que foi lançado, pode-se afirmar que o ângulo entre o vetor velocidade média e o vetor aceleração média é:

Considere as seguintes afirmações sobre os vetores velocidade e aceleração de uma partícula em movimento:

o vetor velocidade pode ser nulo e o vetor aceleração ser diferente de zero.

O módulo do vetor velocidade pode ser constante, com o vetor velocidade mudando com o tempo.

O vetor velocidade pode ser constante mas seu módulo variar com o tempo.

O módulo do vetor velocidade é constante quando o vetor aceleração é sempre perpendicular ao vetor velocidade.

São verdadeiras as afirmações:

1. Todas as afirmações;
2. , e ;
3. , e ;
4. e ;
5. Nenhuma das afirmações anteriores.

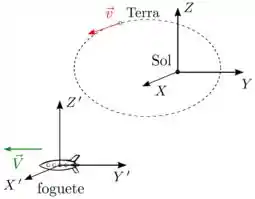
Vista de um referencial fixo nas estrelas e centrado no Sol, a Terra tem vetor velocidade dado em um certo instante por e um foguete em translação tem velocidade constante , como mostra a figura. Considerando o foguete como um referencial com eixos coordenados , , e de mesmas direções e sentidos que os respectivos eixos , e , o vetor velocidade da Terra relativo a ele é

Uma partícula desloca-se ao longo do eixo , de unitario , sob ação de uma força conservativa , correspondente ao potencial , dado pelo gráfico da figura. Para este potencial, entre as alternativas abaixo, a única INCORRETA é

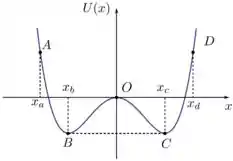
1. Na posição a força sobre a particula é nula;
2. Nas posições e tem-se a condição de equilíbrio estável;
3. No deslocamento da particular de para o trabalho realizado pela força é negativo;
4. No deslocamento da partícula de para a variação da energia cinética é ;
5. Na posição o sentido da força é positivo.

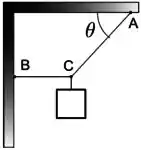
Dois fios ideais e estao presos a um teto horizontal e a uma parede vertical nos respectivos pontos e , como indica a figura. Na extremidade comum dos fios está suspenso e em equilíbrio um bloco de peso . O fio é perpendicular à parede e o fico faz um ângulo com o teto . O módulo da tensão no fio é igual a

Em uma balança dentro de um elevador em movimento vertical é colocado um bloco de massa e a balança indica sobre seu prato uma força vertical de módulo exercida pelo bloco. Em relação a sistema de eixos , fixo na Terra, com vertical orientado para cima a aceleração do elevador é dada por uma componente igual a

1. ;
2. ;
3. ;
4. ;
5. Todas as opções acima estão erradas.

Uma partícula move-se no plano horizontal sob a ação de uma força constante . Em um dado instante a sua posição é e em um instante posterior a sua posição é , onde e são constantes. O trabalho realizado por essa força do instante inicial ao final é

1. ;
2. ;
3. ;
4. ;
5. ;

Dois blocos de massas e estão em movimento retilíneo sobre uma superfície horizontal sem atrito e ligados por um fio ideal horizontal que se mantém tenso durante o movimento.Sobre os blocos agem forças constante na direção do movimento, como mostra a figura. O módulo da tensão do fio é

1. ;
2. ;
3. ;
4. ;
5. ;

Uma partícula de massa é suspensa por uma mola ideal de constante elástica presa no teto. A particula gira em movimento circular uniforme horizontal, de raio e centrado na vertical que passa pelo ponto de suspensão da mola no teto, como indica a figura. A mola mantém-se reta e distendida de um comprimento (a ser determinado). A reta que passa pelo ponto de suspensão da mola e a particual mantém um ângulo constante com a vertical, descrevendo uma superfície cônica no espaço. Considere como dados , , , e o módulo da aceleração da gravidade.

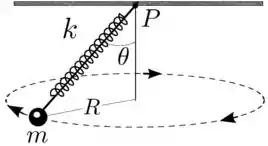
1. Represente em um diagrama as forças que agem sobre a partícula em um instante arbitrário.
2. Calcule a distensão da mola.
3. Determine o módulo da velocidade da partícula.

A figura mostra o perfil suave de uma calha com um trecho inclinado , seguido de um trecho horizontal , que é seguido de um outro trecho inclinado ; as alturas do ponto e do ponto acima do solo são iguais a e o comprimento do trecho horizontal é igual a . Um bloco de massa e dimensões desprezíveis desce a partir do ponto , onde o módulo da sua velocidade é e percorre os trechos , e . O coeficiente de atrito cinético entre o bloco e a calha no trecho é , e entre o bloco e a calha nos trechos e é zero. Considerando como dados , , e o módulo da aceleração da gravidade, calcule:

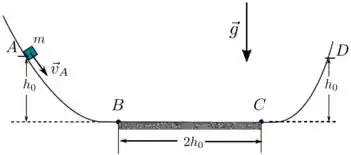
1. Os trabalhos das forças peso e normal nos trechos , e ;
2. O trabalho da força de atrito no trecho ;
3. A variação da energia cinética do ponto ao ponto e o módulo da velocidade do bloco em ;

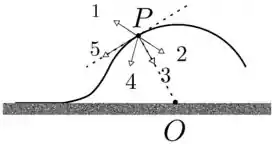
Um carro, considerável como uma partícula, sobre uma lombada circular de centro de curvatura em , como indica a figura. O módulo da velocidade do carro vai diminuindo à medida que ele sobe a lombada. Dadas as setas identificadas pelos números , , , e da figura, a que pode representar a aceleração do carro o ponto da subida indicado é a número