A figura mostra o perfil suave de uma calha com um trecho inclinado , seguido de um trecho horizontal , que é seguido de um outro trecho inclinado ; as alturas do ponto e do ponto acima do solo são iguais a e o comprimento do trecho horizontal é igual a . Um bloco de massa e dimensões desprezíveis desce a partir do ponto , onde o módulo da sua velocidade é e percorre os trechos , e . O coeficiente de atrito cinético entre o bloco e a calha no trecho é , e entre o bloco e a calha nos trechos e é zero. Considerando como dados , , e o módulo da aceleração da gravidade, calcule:
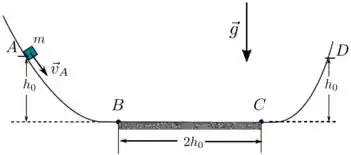
- Os trabalhos das forças peso e normal nos trechos , e ;
- O trabalho da força de atrito no trecho ;
- A variação da energia cinética do ponto ao ponto e o módulo da velocidade do bloco em ;
Passo 1
Vamos começar escrevendo os dados da questão
Vamos fazer isso para verificar depois cada resposta para ver se está de acordo com os dados do problema.
Passo 2
a)
Já vimos que com ao normal é sempre perpendicular a superfície o trabalho dela será zero.
Passo 3
Para calcularmos o trabalho da força peso, devemos nos preocupar apenas com o deslocamento vertical, então
Ele será positivo porque o peso está no sentido do deslocamento vertical
Nesse trecho não temos deslocamento vertical
Ele será negativo porque o peso está no sentido contrário do deslocamento vertical
Passo 4
b)
O trabalho da é negativo porque ele é contra o movimento.
Já vimos em muitos outros exercícios que, no caso do bloco no plano
Então
Passo 5
c)
Pelo teorema trabalho-energia cinética
Onde
Então
Passo 6
Para achar a velocidade vamos achar a variação de energia cinética pela fórmula da energia cinética