P2 de Física 1 da USP - 2013

Um patinador de massa , carregando uma bola de massa , vai em direção a uma parede com velocidade . Num dado instante, ele lança a bola perpendicularmente contra a parede, com velocidade em relação ao solo. Esta rebate na parede e volta nas mãos do patinador. Considere a colisão da bola com a parede perfeitamente elástica e despreze o atrito entre o piso e o patinador, assim como o efeito da gravidade sobre a trajetória da bola.

Qual é a velocidade do patinador após lançar a bola?

Qual é a velocidade do patinador após agarrar a bola rebatida pela parede?

Um sistema massa-mola consiste de uma partícula de massa presa a uma mola de constante elástica e massa desprezível. Montamos este sistema sobre uma plataforma móvel de massa conforme mostrado na figura. A posição de equilíbrio coincide com centro de plataforma, conforme mostra a figura , e tanto a massa se desloca sem atrito sobre a plataforma, quanto a plataforma se desloca sem atrito sobre a superfície horizontal. Suponhamos que a mola seja distendida em e solta, com o sistema todo inicialmente em repouso.

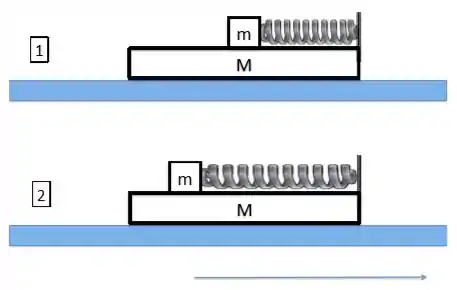
O deslocamento da plataforma, quando a mola estiver comprimida em ,

A velocidade (módulo e sentido) do bloco de massa nesta condição.

A velocidade (módulo e sentido) da plataforma nesta condição.

Uma mola, de comprimento natural e constante elástica , é montada no interior de um aro circular vertical de raio . Uma das extremidades da mola está fixa no ponto e a outra está livre no ponto mais baixo do aro. Um bloco de massa é empurrado contra a mola, que se desloca ao longo da curva em um arco de ângulo , até o ponto , como mostrado na figura. O bloco é então liberado, a partir do repouso. O atrito entre o bloco e o aro é desprezível. Adote o referencial da figura, com origem em .

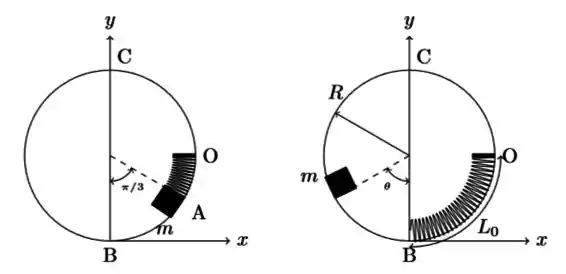
Obtenha uma expressão para a energia mecânica do bloco no ponto em termos de , , , e .

Determine o valor mínimo de para que o bloco consiga executar a curva completa, passando pelo ponto sem cair.

Sabendo-se que a partícula possui energia mecânica no ponto , obtenha uma expressão para a velocidade do bloco no trecho em função do ângulo , , , e .

Dado: , .