Energia Potencial e Conservação de Energia, Movimento Circular
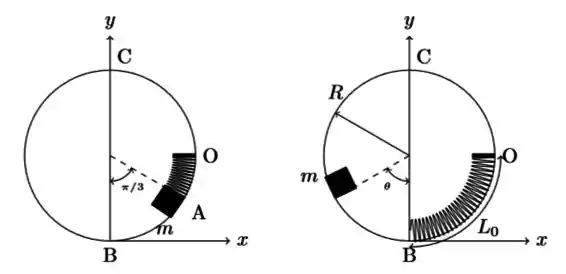
Uma mola, de comprimento natural e constante elástica , é montada no interior de um aro circular vertical de raio . Uma das extremidades da mola está fixa no ponto e a outra está livre no ponto mais baixo do aro. Um bloco de massa é empurrado contra a mola, que se desloca ao longo da curva em um arco de ângulo , até o ponto , como mostrado na figura. O bloco é então liberado, a partir do repouso. O atrito entre o bloco e o aro é desprezível. Adote o referencial da figura, com origem em .
Obtenha uma expressão para a energia mecânica do bloco no ponto em termos de , , , e .
Determine o valor mínimo de para que o bloco consiga executar a curva completa, passando pelo ponto sem cair.
Sabendo-se que a partícula possui energia mecânica no ponto , obtenha uma expressão para a velocidade do bloco no trecho em função do ângulo , , , e .
Dado: , .
Passo 1
No ponto temos energia potencial gravitacional e energia potencial elástica:
Primeiro precisamos descobrir quanto vale . Observando a circunferência com carinho e o ângulo que o bloco faz com o centro vemos que:
Ainda falta descobrirmos quanto vale , que é justamente quanto a mola se comprimiu. Pela figura vemos que ela se comprimiu uma distancia equivalente ao comprimento de uma seção da circunferência. Podemos encontrar essa seção fazendo:
Agora sim! Já temos tudo que precisamos. Vamos substituir na equação da energia.
Passo 2
Bem, para chegar até o ponto , o corpo precisara ter energia potencial gravitacional e energia cinética suficiente.
Para que o bloco não perca o contato com a circunferência no ponto , devemos ter pelo menos a força centrípeta idêntica ao peso.
Agora podemos substituir na equação de energia do ponto .
Agora, para achar o valor de , basta igualar a energia do ponto com a energia do ponto , utilizando o principio de conservação de energia mecânica.
Passo 3
Energia mecânica no trecho :
Aplicando conservação de energia mecânica