Sistema de Partículas, Forças e Leis de Newton, Energia Potencial e Conservação de Energia
Um sistema massa-mola consiste de uma partícula de massa presa a uma mola de constante elástica e massa desprezível. Montamos este sistema sobre uma plataforma móvel de massa conforme mostrado na figura. A posição de equilíbrio coincide com centro de plataforma, conforme mostra a figura , e tanto a massa se desloca sem atrito sobre a plataforma, quanto a plataforma se desloca sem atrito sobre a superfície horizontal. Suponhamos que a mola seja distendida em e solta, com o sistema todo inicialmente em repouso.
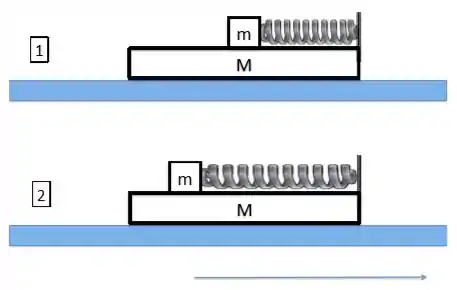
O deslocamento da plataforma, quando a mola estiver comprimida em ,
A velocidade (módulo e sentido) do bloco de massa nesta condição.
A velocidade (módulo e sentido) da plataforma nesta condição.
Passo 1
Lembrando que o centro de massa pode ser calculado pela fórmula:
Vamos convencionar a posição , que é a posição da mola relaxada, como o ponto de origem. Ou seja, o corpo de massa terá sempre o vetor posição nulo, visto que seu centro de massa coincide com o ponto que adotamos como origem.
Em um primeiro momento, a mola é distendida de , ou seja, posição .
Agora, o bloco é solto e chega a comprimir a mola de , ou seja, chega até a posição .
Logo, o deslocamento da plataforma será a variação da posição do centro de massa.
Passo 2
Aplicando a conservação do momento linear:
Entretanto, no primeiro momento, tanto o bloco quanto a plataforma estão em repouso. Portanto , ficamos então com:
Agora aplicando a conservação de energia mecânica. No primeiro momento temos apenas a energia potencial elástica no ponto . No segundo momento, além da energia potencial elástica no ponto , temos também a energia cinética do bloco e da plataforma. Passamos a posição de para , justamente porque temos que .
Substituindo os valores:
Lembrando que .
Passo 3
No item anterior, descobrimos que:
Logo:
O negativo, significa que ela tem sentido contrário ao do bloco.