P3 de Física 1 da USP - 2014

Imagine que um objeto de perfil circular (com raio , massa e momento de inércia ) seja colocado no ponto da canaleta ilustrada abaixo com velocidade inicial nula. O atrito entre esse objeto e a canaleta é suficiente para que ele role sem deslizar e a resistência do ar é desprezível.

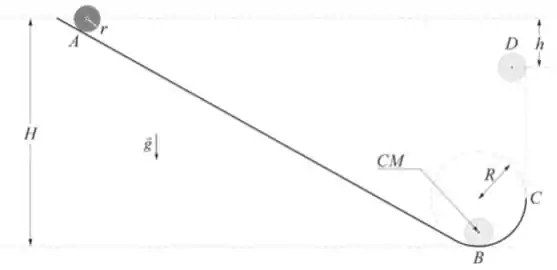
Esboce o diagrama das forças que agem sobre o objeto quando ele está no ponto da trajetória e escreva as equações do movimento, de translação e de rotação (não é necessário resolvê-las).

O ponto da trajetória indica o ponto mais alto que o objeto atinge após ser atirado verticalmente para cima, em . Explique em até duas linhas legíveis porque a velocidade angular do objeto, em torno do seu centro de massa, em e em são iguais.

Considere os seguintes perfis de densidade para o objeto (quanto mais escuro, mais denso), todos com a mesma massa. Liste-os, em ordem crescente de momento de inércia.

Para qual dos perfis acima o corpo sobe mais (ou seja, a distância é menor)?

Calcule a altura em função dos parâmetros , , , e .

Considere um sistema de cinco objetos puntiformes dispostos em um plano de acordo com a figura a seguir. Cada um dos quatro objetos periféricos possui massa igual a , enquanto que o quinto, localizado na origem do sistema de coordenadas indicado na figura, tem massa . Eles são unidos por hastes rígidas e de massas desprezíveis.

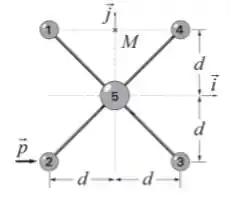
Calcule o momento de inércia do sistema em relação ao eixo passando pelos objetos e .

Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pela origem.

Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pelo ponto indicado na figura.

O sistema, inicialmente em repouso, recebe um impulso conforme ilustra a figura. Qual é a velocidade subsequente do centro de massa? Escreva sua resposta em função de , e .

Ainda considerando a situação descrita no item anterior, qual é a velocidade angular do sistema, em torno de seu centro de massa, imediatamente após o impulso? Escreva sua resposta em função de , e .

Após o impulso o sistema passa a rodar no sentido anti-horário do plano. Seja e . Obtenha o módulo e o sentido do torque aplicado no sistema por uma força resistiva, sabendo que a velocidade angular decresce linearmente de até em segundos.

Considere um projétil de massa movimentando-se no plano de um sistema de coordenadas nas situações descritas pelos itens abaixo. Adotamos nesta questão um sistema de unidades arbitrário, onde a constante gravitacional de Newton é igual a . Expresse seus resultados em função de onde for necessário.

O projétil desloca-se isoladamente em movimento retilíneo uniforme. Sua posição em função do tempo é dada por onde e são os versores dos eixos e , respectivamente. Qual é o módulo e o sentido do vetor momento angular do projétil com relação à origem desse sistema de coordenadas? Justifique.

Nos itens subsequentes, considere um planeta de massa , com , fixo na origem do sistema de coordenadas. Para os itens , e , o planeta é puntiforme e a condição inicial do projétil é e .

Determine o vetor momento angular e a energia total do projétil.

Qual é a forma geométrica que descreve a trajetória? Justifique. Dica: ache o raio de equilíbrio minimizando o potencial efetivo e tire suas conclusões.

Faça um esboço bem qualitativo da trajetória do projétil com relação à posição do planeta indicando, em dois pontos distintos da trajetória, as orientações dos versores das coordenadas polares.

O planeta agora é uma esfera de raio com densidade que varia radialmente de a de acordo com

Ou seja, é mais denso em seu centro do que em sua superfície. O projétil agora encontra-se em repouso na superfície do planeta. Partindo da equação da energia total do projétil obtenha a velocidade mínima, em termos de , para que o projétil escape para bem longe do planeta (velocidade de escape).