Imagine que um objeto de perfil circular (com raio , massa e momento de inércia ) seja colocado no ponto da canaleta ilustrada abaixo com velocidade inicial nula. O atrito entre esse objeto e a canaleta é suficiente para que ele role sem deslizar e a resistência do ar é desprezível.
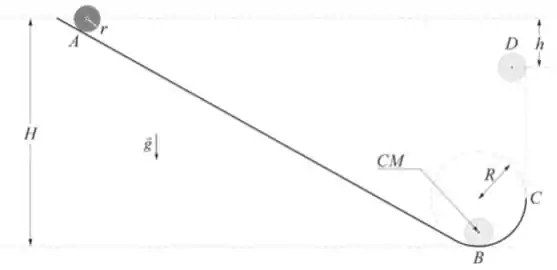
Esboce o diagrama das forças que agem sobre o objeto quando ele está no ponto da trajetória e escreva as equações do movimento, de translação e de rotação (não é necessário resolvê-las).
O ponto da trajetória indica o ponto mais alto que o objeto atinge após ser atirado verticalmente para cima, em . Explique em até duas linhas legíveis porque a velocidade angular do objeto, em torno do seu centro de massa, em e em são iguais.
Considere os seguintes perfis de densidade para o objeto (quanto mais escuro, mais denso), todos com a mesma massa. Liste-os, em ordem crescente de momento de inércia.

Para qual dos perfis acima o corpo sobe mais (ou seja, a distância é menor)?
Calcule a altura em função dos parâmetros , , , e .
Passo 1
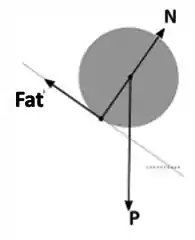
Bom visto que o corpo não possui movimento na vertical, ao decompor a força Peso podemos construir a relação:
Sendo θ o ângulo de inclinação entre o plano e a horizontal.
Aplicando a segunda lei de Newton na horizontal :
Aplicando a Lei de rotação :
Apenas a força de atrito faz torque no objeto. Lembrando que o torque nada mais é que o produto vetorial entre a força aplicada e a distância do ponto de aplicação ao eixo de rotação.
Passo 2
Basta lembrar que:
Ou seja, A partir do ponto , a força de atrito que produzia torque no objeto não existe mais, e se não tiver torque, o momento angular tem que ser constante. Lembrando que , e que o momento de inercia é constante. Logo, a velocidade angular obrigatoriamente tem que ser constante!
Passo 3
Visto que o momento de inércia é calculado por:
Para maximizar o momento de inércia, pela fórmula, o vetor (distância ao eixo de rotação) precisa ser o maior possível considerando objetos de mesma massa.
Logo, quanto mais massa concentrada próxima ao eixo de rotação, menor o momento de inércia.
Temos então a ordem dos perfis: 2, 3, 1 e 4.
Passo 4
Utilizando a conservação de energia mecânica do ponto ao temos que:
Então observamos que se a energia de rotação diminuir, isso terá que ser compensado com um aumento na energia potencial, diminuindo .
Logo, para diminuir a energia de rotação precisamos escolher o objeto com o menor momento de inércia, que é o perfil 2.
Passo 5
A energia mecânica do objeto nos pontos da canaleta são:
Utilizando a condição de não deslizamento e lembrando que (item ), as expressões podem ser reescritas assim:
Como a força gravitacional é conservativa e a força de atrito, responsável pelo rolamento do objeto, não realiza trabalho (pois não há deslizamento), a energia mecânica é conservada. Logo, . Para obter a altura igualamos as energias em e em :
Mas ainda não conhecemos . Para isso, escrevemos:
Substituindo em :
Dividindo o numerador e denominador por :
Resposta
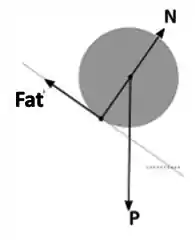
Translação:
Rotação:
A partir do ponto , a força de atrito que produzia torque no objeto não existe mais, logo o momento angular tem que ser constante e a velocidade angular obrigatoriamente tem que ser constante.