P-REC de Física 1 da USP - 2022

Enunciado das questões Q1 e Q2

Uma partícula move-se em um plano horizontal com velocidade constante . Ao passar pelo ponto de coordenadas , no instante , ela passa a sofrer uma aceleração constante .

Q1

Em que instante a partícula passa por ? Dê sua resposta em segundos.

a) 2,0

b) 3,0

c) 4,0

d) 5,0

e) 6,0

Enunciado das questões Q1 e Q2

Uma partícula move-se em um plano horizontal com velocidade constante . Ao passar pelo ponto de coordenadas , no instante , ela passa a sofrer uma aceleração constante .

Q2

Qual é a distância que a partícula está em relação à origem do sistema de coordenadas, quando ? Dê sua resposta em metros.

a) 40

b) 50

c) 60

d) 70

e) 80

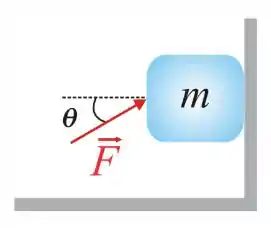
Um bloco de massa é empurrado contra uma parede por uma força que faz um ângulo com a horizontal, como mostra a figura. Se o coeficiente de atrito estático entre a superfície da parede e o bloco vale , calcule qual é o valor mínimo do módulo de que faz que o bloco permaneça estacionário. Dê sua resposta em Newtons.

Adote .

a)

b)

c)

d)

e)

Um bloco de massa , que repousa sobre uma superfície horizontal lisa, é ligado a um bloco de massa por uma corda leve que passa por uma polia de massa desprezível, que pode girar sem atrito. O bloco de massa está ligado a uma mola de constante elástica que tem uma das extremidades fixa em uma parede vertical como mostra a figura. Se os blocos são liberados a partir do repouso com a mola na posição relaxada, calcule qual é a maior velocidade atingida pelos dois blocos. Dê sua resposta em metros por segundo.

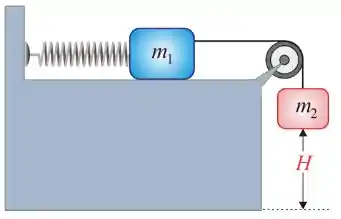
Considere os blocos como partículas.

Máximos e Mínimos de uma função são caracterizados pelo fato de que a derivada da função se anula em tais pontos.

Adote para a aceleração da gravidade

a)

b)

c)

d)

e)

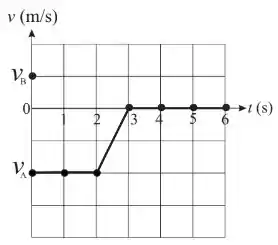
Duas partículas e , de massas e , interagem apenas entre si no intervalo . Elas deslocam-se em cima de uma mesa horizontal sem atrito ao longo do eixo . No instante , a partícula tem velocidade inicial enquanto a partícula tem velocidade inicial . Durante o intervalo de tempo observa-se, a cada segundo, a velocidade da partícula . O gráfico mostra a função obtida unindo-se por segmentos de reta os pontos experimentais representados por pequenos círculos.

Q5. Com base nos dados, determine a força média exercida pela partícula na partícula durante o tempo de colisão.

a)

b)

c)

d)

e)

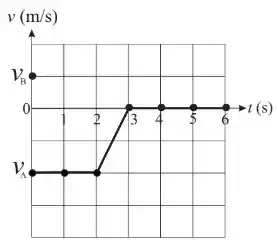
Duas partículas e , de massas e , interagem apenas entre si no intervalo . Elas deslocam-se em cima de uma mesa horizontal sem atrito ao longo do eixo . No instante , a partícula tem velocidade inicial enquanto a partícula tem velocidade inicial . Durante o intervalo de tempo observa-se, a cada segundo, a velocidade da partícula . O gráfico mostra a função obtida unindo-se por segmentos de reta os pontos experimentais representados por pequenos círculos.

Q6. Com base nos dados, determine a energia cinética do sistema formado pelas duas partículas quando e qual foi o tipo de colisão.

a)

b)

c)

d)

e)

Um disco homogêneo, de massa e raio , move-se no plano horizontal em rotação pura ao redor do eixo vertical fixo , que tangencia a borda do disco e é perpendicular ao plano . O vetor momento angular do disco, em relação à origem do sistema de coordenadas, é dado por , em unidades do SI. Se em , o disco está girando com velocidade angular , podemos afirmar que o seu raio , em centímetros, é:

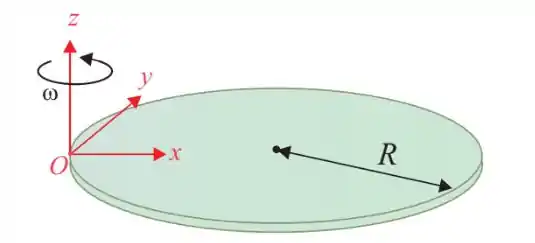
O momento de inércia de um disco de massa e raio em relação ao eixo de rotação que passa pelo seu centro de massa e é perpendicular ao plano é

a)

b)

c)

d)

e)

Uma bola homogênea (esfera) de raio , rola sem escorregar por um tobogã com um único de raio , como mostra a figura. A bola parte do repouso, com seu centro de massa na altura acima da base. Qual é o valor mínimo de para que a bola passe ponto no topo da volta fechada? Dê sua resposta em unidades do Sistema Internacional (SI).

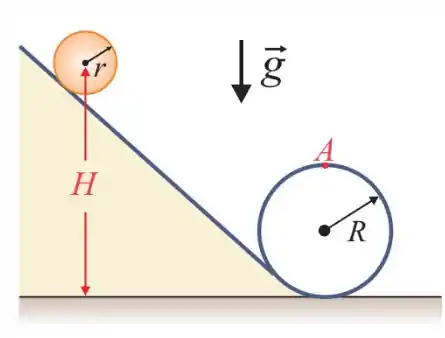
O momento de inércia de uma esfera de massa e raio em relação ao eixo de rotação que passa pelo seu centro de massa e é perpendicular ao plano da página é

a)

b)

c)

d)

e)