Corpos Rígidos, Momento Linear, Rotação, Dinâmica de Rotação
Considere um sistema de cinco objetos puntiformes dispostos em um plano de acordo com a figura a seguir. Cada um dos quatro objetos periféricos possui massa igual a , enquanto que o quinto, localizado na origem do sistema de coordenadas indicado na figura, tem massa . Eles são unidos por hastes rígidas e de massas desprezíveis.
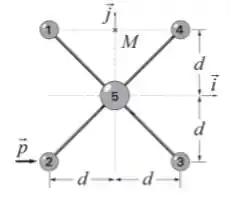
Calcule o momento de inércia do sistema em relação ao eixo passando pelos objetos e .
Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pela origem.
Calcule o momento de inércia do sistema em relação ao eixo perpendicular ao plano da figura e passando pelo ponto indicado na figura.
O sistema, inicialmente em repouso, recebe um impulso conforme ilustra a figura. Qual é a velocidade subsequente do centro de massa? Escreva sua resposta em função de , e .
Ainda considerando a situação descrita no item anterior, qual é a velocidade angular do sistema, em torno de seu centro de massa, imediatamente após o impulso? Escreva sua resposta em função de , e .
Após o impulso o sistema passa a rodar no sentido anti-horário do plano. Seja e . Obtenha o módulo e o sentido do torque aplicado no sistema por uma força resistiva, sabendo que a velocidade angular decresce linearmente de até em segundos.
Passo 1
O momento de inércia em corpos pontuais pode ser encontrado da seguinte forma:
Como o eixo de rotação está passando pelos objetos 2 e 3, temos que as distâncias até o eixo de rotação serão:
Logo:
Passo 2
Temos agora o eixo passando perpendicularmente ao objeto 5. Então os vetores posições serão agora:
Passo 3
Utilizando o teorema dos eixos paralelos:
Onde é o momento de inércia do item anterior.
Logo:
Passo 4
Aplicando a fórmula do momento linear:
Passo 5
Calculando o momento angular por:
Ou seja, produto vetorial entre o momento linear e a distância ao eixo, que no nesse caso como o eixo é perpendicular ao objeto 5, a distância é , portanto:
Entretanto também temos outra forma de calcular o momento angular:
Lembrando que estamos usando o eixo perpendicular ao objeto 5, então:
Agora podemos igualar os dois valores de
Passo 6
Como decresce linearmente, temos constante. Logo, podemos utilizar:
Com os valores fornecidos para e temos:
Lembrando que o torque pode ser calculado por:
Temos: