3º EE de Física 2 da UFPE - 2016.1

Dois gases distintos são mantidos isolados por recipientes rígidos e . O recipiente contém do gás He enquanto o recipiente contém 1 mol do gás . Admita que os gases são ideais e que suas temperaturas são e , respectivamente. Nestas temperaturas as oscilações internas não contribuem para energia média. Considere que as moléculas diatômicas possuem movimento rotacional e assuma que a constante dos gases ideais é dada por

I) A energia interna do gás em é

II) A energia interna do gás em é .

III) Se os gases são postos em contato térmico, permanecendo isolados do ambiente a temperatura final de equilíbrio será .

IV) A contribuição da rotação para energia interna é nula para o gás em A.

V) Em baixas temperaturas, onde somente a energia de translação contribui para a energia interna, a energia interna por mol é maior para o devido à maior massa.

Assinale a alternativa correta:

a) As afirmações I, II e V são verdadeiras.

b) Somente as afirmações I e IV são verdadeiras

c) Somente as afirmações I, II e IV são verdadeiras

d) As afirmações I, III, V são falsas.

e) Somente a informação III é falsa

A figura ao lado mostra um ciclo reversível ao qual são submetidos de um gás ideal monoatômico. No ponto a pressão e o volume são e e no ponto são e respectivamente. Analise as afirmações abaixo:

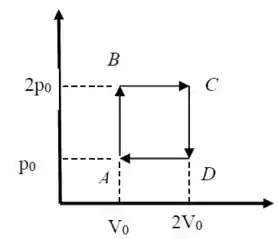
I)A temperara

II) O calor recebido pelo sistema no processo é

III)A eficiência de um ciclo de Carnot que operasse entre as temperaturas mais baixa e mais alta do ciclo mostrado na figura seria .

IV) A eficiência no ciclo da figura é menor que

V)A variação da entropia no processo é

Assinale a alternativa correta:

a) Somente as afirmações I e III são falsas.

b)A afirmações I, IV e V são falsas.

c)As afirmações I, II, III são verdadeiras.

d)Somente a afirmações I e II são verdadeiras.

e)Todas as afirmações são verdadeiras

A figura mostra três placas metálicas retangulares. Suas dimensões estão especificadas, sendo (Placa 1), (Placa 2) e (Placa 3), bem como seus respectivos coeficiente de expansão linear: ,e . Se todas sofrem a mesma variação de temperatura, assinale a opção correta:

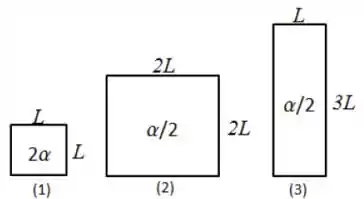
a) A dimensão vertical da placa 1 é a que mais aumenta e a área da placa 3 é a que mais aumenta;

b) A dimensão vertical da placa 2 é a que mais aumenta e a área da placa 1 aumenta tanto quanto a área da placa 2;

c) A dimensão vertical da placa 3 é a que mais aumenta e a área da placa 1 é a que mais aumenta;

d) A dimensão vertical da placa 1 é a que mais aumenta e a área da placa 2 aumenta tanto quanto a área da placa 1;

e) A dimensão vertical da placa 3 é a que mais aumenta e a área da placa 2 é a que mais aumenta.

A figura mostra o ciclo termodinâmico a que é submetido de um gás ideal diatômico (5 graus de liberdade). As temperaturas são , e . Determine, em função da constante universal dos gases :

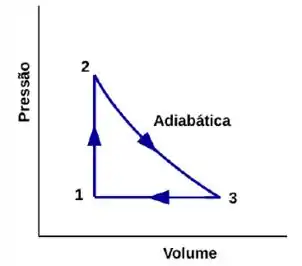
a) O calor trocado a variação de energia interna e o trabalho realizado para a trajetória 1→2.

b) O calor trocado , a variação de energia interna e o trabalho realizado para a trajetória 2→3.

c) O calor trocado , a variação de energia interna e o trabalho realizado para a trajetória 3→1.

d) O calor trocado, a variação de energia interna e o trabalho realizado para o ciclo completo.

A figura mostra uma parede composta de três materiais diferentes, com espessuras idênticas e com condutividade térmicas . A transferência de energia através delas sob a forma de calor é não-nula e em regime estacionário. Assinale a alternativa correta quanto à taxa de condução e à diferença de temperatura entre os materiais.

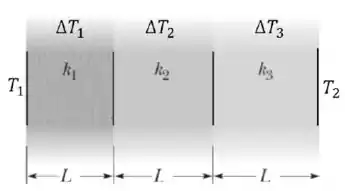
O ciclo de combustão interna de um motor a gasolina dos carros é conhecido como ciclo de Otto. O ciclo opera entre quatro processos, dois isocóricos (volume constante), onde ocorrem as trocas de calor, intercalados por dois adiabáticos, sem trocas de calor. No processo ocorre a queima do combustível na explosão fazendo com que a temperatura varie, e no processo ocorre o escape dos gases produtos da queima, variando a temperatura de . Supondo que os processo seja quase estáticos e que o gás seja ideal o ciclo é representado na figura ao lado num diagrama.

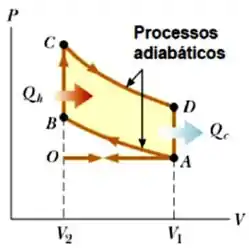
a) Determine o rendimento do ciclo de Otto, em termos de 𝑒

b) Sabendo que um processo adiabático obedece à e considerando escreva a resposta anterior em termos de .

c) Calcule a variação de entropia, , nos processos, e no ciclo completo utilizando a variação de entropia encontrada em cada processo.

d) Represente o ciclo de Otto num diagrama .