Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Variação da Entropia de um Gás Ideal

Ver Teoria
Exercício 33123456789101112131415161718192021222324252627282930313234353637383940414243444546474849505152535455565758596061626364

Enunciado

Origem do Exercício

A figura ao lado mostra um ciclo reversível ao qual são submetidos 2   m o l e s de um gás ideal monoatômico. No ponto A a pressão e o volume são V 0 e p 0 e no ponto C   são 2 V 0 e 2 p 0 respectivamente. Analise as afirmações abaixo:

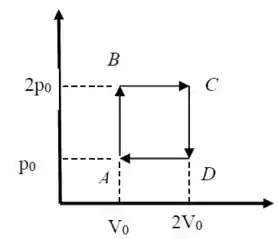
I)A temperara T D   =   2 T A  

II) O calor recebido pelo sistema no processo A B   é 3 R T A

III)A eficiência de um ciclo de Carnot que operasse entre as temperaturas mais baixa e mais alta do ciclo mostrado na figura seria 0,75 .

IV) A eficiência no ciclo da figura é menor que 0,1

V)A variação da entropia no processo A B C   é 4 R l n 2

Assinale a alternativa correta:

a) Somente as afirmações I e III são falsas.

b)A afirmações I, IV e V são falsas.

c)As afirmações I, II, III são verdadeiras.

d)Somente a afirmações I e II são verdadeiras.

e)Todas as afirmações são verdadeiras

Passo 1

Vamos analisar uma por uma:

  1. Basta a gente aplicar a equação dos gases:

    2. P V = n R T → T = P V n R

    Assim:

    T A = p 0 V 0 n R

    E:

    T B = p 0 2 V 0 n R = 2 p 0 V 0 n R = 2 T A

    Assim, a afirmação está correta.

  2. A transferência ocorre à volume constante, assim:

    3. Q A B = n c v T B - T A

    Calculando a temperatura T B :

    T B = P B V B n R = 2 p 0 V 0 n R = 2 T A

    Lembrando que n = 2 e c v = 3 2 R ( monoatômico):

    Q A B = 2 3 2 R 2 T A - T A = 3 R T A

    Está correta!!!

    Passo 2

  3. Basta a gente usar a equação da eficiência para uma máquina de Carnot:

    4. e = 1 - T F T Q

    A temperatura da fonte fria vai ser a menor temperatura do ciclo. Essa temperatura ocrre em A , assim:

    T A = p 0 V 0 n R

    E a maior temperatura vai ser a temperatura em C :

    T C = 2 p 0 2 V 0 n R = 4 T A

    Assim:

    e = 1 - T C T A = 1 - 1 4 = 0,75

    Passo 3

  4. Agora a gente vair ter que calcular a eficiência na força bruta, isso é, usando:

    5. e = W t o t a l Q a b s o r v i d o

    O calor absorvido é dado por:

    Q a b c = Q a b + Q b c

    ∴

    Q a b = 3 R T A

    ∴

    Q b c = n c p T C - T B = 2 5 R 2 4 T A - 2 T A = 10 R T A

    Assim:

    Q a b c = 3 R T A + 10 R T A = 13 R T A

    O trabalho total será fácil de calcular, já que o trabalho em dois trechos, A B   e   C D , é nulo( transformações isocóricas):

    W t o t a l = W A B + W B C + W C D + W D A = W A B + W D A

    Os dois trabalhos são à pressão constante:

    W t o t a l = 2 p 0 2 V 0 - V 0 + p 0 V 0 - 2 V 0 = 2 p 0 V 0 - p 0 V 0 = p 0 V 0

    Usando a equação dos gases:

    p 0 V 0 = n R T A

    ∴

    W t o t a l = n R T A = 2 R T A

    Assim:

    e = 2 R T A 13 R T A = 2 13 = 0,154 > 0,1

    Logo a afirmação está incorreta.

  5. A variação de entropia em A B C será dada por:

∆ S A B C = ∆ S A B + ∆ S B C

Onde:

∆ S A B = ∫ T A T B Q T = ∫ T A T B n c v d T T = n c v ln ⁡ T B T A = 2 . 3 R 2 ln ⁡ 2 T A T A = 3 R l n 2

E:

∆ S B C = ∫ T B T C n c p d T T = n c p ln ⁡ T C T B = 2 . 5 R 2 ln ⁡ 4 T A 2 T A = 5 R l n 2

Assim:

∆ S A B C = ∆ S A B + ∆ S B C = 3 R l n 2 + 5 R l n 2 = 8 R l n 2

Assim, a afirmação está incorreta.

Resposta

c)

Exercícios de Livros Relacionados

Suponha que 1 m o l de um gás monoatômico ideal inicialmente à pressão p 1 e ocupando um volume V 1 seja submetido sucessivamente a dois processos: ( 1 ) uma expansão isotérmica até um volume 2 V 1 e
Suponha que 0,55 m o l de um gás ideal seja expandido isotérmica e reversivelmente nas quatro situações da tabela abaixo. Qual é a variação da entropia do gás para cada situação?
Quanta energia deve ser transferida na forma de calor para uma expansão isotérmica reversível de um gás ideal a 132 ° C se a entropia do gás aumenta de 46,0J / K ?
Suponha que 4,00m o l s de um gás ideal sofrem uma expansão reversível isotérmica do volume V 1 para o volume V 2 = 2,00 V 1 a uma temperatura T = 400K . Determine (a) o trabalho realizado pelo gás e
Uma caixa de 1,0 L contém N moléculas de um gás ideal, e as posições das moléculas são observadas 100 vezes por segundo. Calcule o temo médio que deve decorrer antes que se possa observar toas as N mo