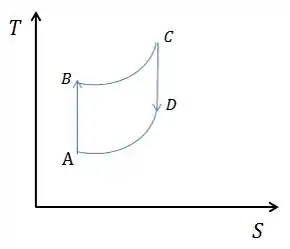
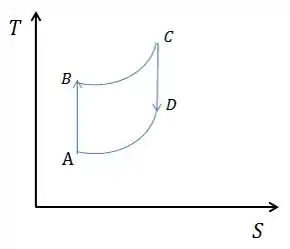
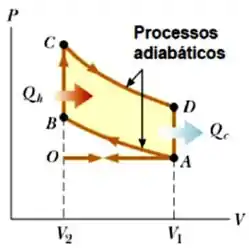
O ciclo de combustão interna de um motor a gasolina dos carros é conhecido como ciclo de Otto. O ciclo opera entre quatro processos, dois isocóricos (volume constante), onde ocorrem as trocas de calor, intercalados por dois adiabáticos, sem trocas de calor. No processo ocorre a queima do combustível na explosão fazendo com que a temperatura varie, e no processo ocorre o escape dos gases produtos da queima, variando a temperatura de . Supondo que os processo seja quase estáticos e que o gás seja ideal o ciclo é representado na figura ao lado num diagrama.
a) Determine o rendimento do ciclo de Otto, em termos de 𝑒
b) Sabendo que um processo adiabático obedece à e considerando escreva a resposta anterior em termos de .
c) Calcule a variação de entropia, , nos processos, e no ciclo completo utilizando a variação de entropia encontrada em cada processo.
d) Represente o ciclo de Otto num diagrama .
Passo 1
a)
Sabendo que em um ciclo, o trabalho pode ser dado por:
Onde é o calor retirado da fonte quente e o calor despejado para a fonte fria. Bom, e onde esses processos ocorrem?
Não podem ocorrer em nem em , já que ali ocorrem transformações adiabáticas. Então só nos resta
Como em existe um aumento de pressão, existe um ganho de energia pelo gás. É natural pensar que ali o calor é trocado. No processo ocorre o contrário, então ali é trocado o calor
Vamos aplicar o módulo e calcular cada um desses calores:
Bom, o rendimento pode ser dado por;
Passo 2
b)
Para o trecho , podemos escrever:
E pro processo
E
Temos que:
Assim:
Assim:
Reescrevendo a eficiência do ciclo:
Passo 3
c)
A variação de entropia de cada trecho será:
As variações nulas ocorrem nas transformações adiabáticas.Assim:
Usando:
Assim:
Assim:
E o do ciclo
E a variação do ciclo completo será:
Passo 4
d)
Os processos são adiabáticos. Neles, não ocorre variação de entropia, assim, a entropia é constante. No diagram, isso vai aparecer como retas verticais.
Já os outros dois processos são logaritimos. Afinal de contas, aparecem logaritmos nas expressões das variações. Assim, no final, o ciclo vai ter uma cara mais ou menos assim: