Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Dilatação Térmica

Ver Teoria
Exercício 1812345678910111213141516171920212223242526272829303132333435

Enunciado

Origem do Exercício

A figura mostra três placas metálicas retangulares. Suas dimensões estão especificadas, sendo L x L   (Placa 1), 2 L x 2 L   (Placa 2) e L x 3 L (Placa 3), bem como seus respectivos coeficiente de expansão linear: 2 α , α 2 e α 2 . Se todas sofrem a mesma variação de temperatura, assinale a opção correta:

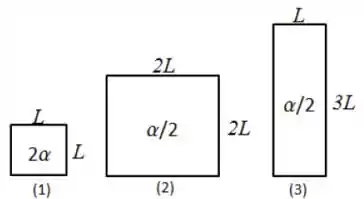
a) A dimensão vertical da placa 1 é a que mais aumenta e a área da placa 3 é a que mais aumenta;

b) A dimensão vertical da placa 2 é a que mais aumenta e a área da placa 1 aumenta tanto quanto a área da placa 2;

c) A dimensão vertical da placa 3 é a que mais aumenta e a área da placa 1 é a que mais aumenta;

d) A dimensão vertical da placa 1 é a que mais aumenta e a área da placa 2 aumenta tanto quanto a área da placa 1;

e) A dimensão vertical da placa 3 é a que mais aumenta e a área da placa 2 é a que mais aumenta.

Passo 1

A questão fala de expansões de dimensões verticais e de áreas. Assim, de início, basta você lembrar que:

β = 2 α

Ou seja, o coeficiente de expansão superficial é o dobre do coeficiente de expansão linear.

Vamos analisar então as expansões lineares e superficias( de área) de cada uma dessas placas.

Passo 2

  1. Placa 1:

    2. A expansão da dimensão vertical vai ser dada por:

    ∆ L 1 = L 0 1 α 1 ∆ T = L 2 α ∆ T

    E a área se expande de acordo com:

    ∆ A 1 = A 0 1 2 α 1 ∆ T = L 2 4 α ∆ T

  2. Placa 2:

    3. ∆ L 2 = L 0 2 α 2 ∆ T = 2 L α 2 ∆ T = L α ∆ T

    ∆ A 2 = A 0 2 2 α 2 ∆ T = 2 L 2 2 . α 2 ∆ T = L 2 4 α ∆ T

    Passo 3

  3. Placa 3:

∆ L 3 = L 0 3 α 3 ∆ T = 3 L α 2 ∆ T = L 3 2 α ∆ T

∆ A 3 = A 0 3 2 α 3 ∆ T = 3 L 2 2 . α 2 ∆ T = L 2 3 α ∆ T

Então, analisando todas essas quantidades, podemos chegar à seguinte conclusão:

“A dimensão vertical da placa 1 é a que mais aumenta e a área da placa 2 aumenta tanto quanto a área da placa 1”.

Assim: d).

Resposta

d)

Exercícios de Livros Relacionados

Determine a variação de volume de uma esfera de alumínio com um raio inicial de 10 c m quando a esfera é aquecida de 0 ° C para 100 ° C
A 20 ° C , uma barra tem exatamente 20,05 c m de comprimento, de acordo com uma régua de aço. Quando a barra e a régua são colocadas em um forno a 270 ° C , a barra passa a medir 20,11 c m de acordo c
Como resultado de um aumento de temperatura de 32 ° C , uma barra com rachadura no centro dobra pra cima . Se a distância fixa L 0 é 3,77 m e o coeficiente de dilatação linear da barra é 25.10 - 6 / °
Qual é o aumento de volume de um cubo de alumínio com 5,00c m de lado quando o cubo é aquecido de 10,0 ° C para 60,0 ° C ?
Três barras retilíneas de mesmo comprimento, feitas de alumínio, Invar e aço, todas a 20,0 ° C , formam um triângulo equilátero com pinos articulados nos vértices. A que temperatura o ângulo oposto à