Origem do Exercício
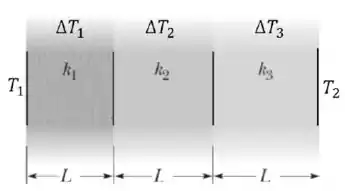
A figura mostra uma parede composta de três materiais diferentes, com espessuras idênticas e com condutividade térmicas . A transferência de energia através delas sob a forma de calor é não-nula e em regime estacionário. Assinale a alternativa correta quanto à taxa de condução e à diferença de temperatura entre os materiais.
Passo 1
Temos três condutores em série. Assim, a condutividade equivalente é dada por:
A potência é dada por:
Como a potência é a mesma nas três placas, podemos pegar uma das diferenças de temperatura e usar no cálculo acima:
Passo 2
Bom, a potência nos três materiais é igual. Assim:
Além disso:
Levando-se em consideração que:
E:
Assim:
Resposta
b)
Exercícios de Livros Relacionados
Um carpinteiro constrói uma porta de madeira maciça com dimensões de 2,0m × 0,95m × 5,0c m . Sua condutividade térmica é k = 0,120 W / m ⋅ K . A película de ar sobre a superfície interna e a película
Pingentes de gelo. A água cobre a superfície de um pingente de gelo ativo (em processo de crescimento) e forma um tubo curto e estreito na extremidade do eixo central (Figura). Como a temperatura da i
A figura mostra uma parede feita de quatro camadas, de condutividades térmicas k 1 = 0,060 W m . K , k 3 = 0,040 W m . K e k 4 = 0,12 W m . K ( k 2 não é conhecida). As espessuras das camadas são L 1
( a ) Calcule a taxa com a qual o calor do corpo atravessa a roupa de um esquiador em regime estacionário, a partir dos seguintes dados: a área da superfície do corpo é 1,8m 2 ; a roupa tem 1,0c m de
Efeito Leidenfrost. Quando se deixa cair uma gota d’água em uma frigideira cuja temperatura está entre 100 ° C e 200 ° C , a gota dura menos de 1s . Entretanto, se a temperatura da frigideira é maior,