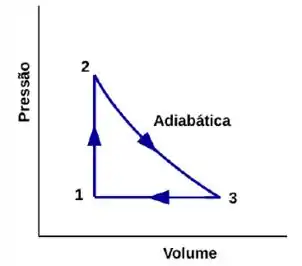
A figura mostra o ciclo termodinâmico a que é submetido de um gás ideal diatômico (5 graus de liberdade). As temperaturas são , e . Determine, em função da constante universal dos gases :
a) O calor trocado a variação de energia interna e o trabalho realizado para a trajetória 1→2.
b) O calor trocado , a variação de energia interna e o trabalho realizado para a trajetória 2→3.
c) O calor trocado , a variação de energia interna e o trabalho realizado para a trajetória 3→1.
d) O calor trocado, a variação de energia interna e o trabalho realizado para o ciclo completo.
Passo 1
- O calor é dado à volume constante:
- Como transformação é adiabática, o calor trocado é nulo:
Perceba que graus de liberdade corresponde ao gás diatômico.
Já o trabalho é nulo, pois a transformação é a volume constante:
Assim, a variação de energia interna é:
Passo 2
Assim:
Usando a expressão da energia interna:
Assim, o trabalho é dado por:
Passo 2
c)
O calor trocado, agora, é à pressão constante, então:
Assim:
E a variação de energia interna será:
Assim, o trabalho será:
Passo 3
d)
O calor total será:
Além disso, em um ciclo a variação da energia interna é sempre nula( já que ela é uma função de estado), assim:
E, por isso: