P1 de Física 3 - FIS1051 da PUCRIO - 2018.2

Parte ) Considere uma esfera isolante, que está mostrada na figura abaixo, de raio e densidade volumétrica de carga , onde é a carga total da esfera isolante. Utilizando a lei de Gauss,

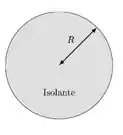
1. Determine o campo elétrico na região .
2. Determine do campo elétrico na região .

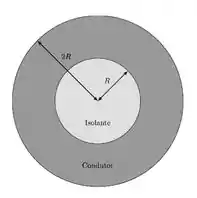
Parte ) Uma esfera isolante de raio foi envolta por uma casca esférica condutora de carga líquida nula. Essa casca esférica, em equilíbrio eletrostático, possui raio interno e raio externo , como mostra a figura abaixo. Nesta situação, considere que a carga total da esfera isolante é , distribuída uniformemente no seu interior.



3. Determine o campo elétrico na região .
4. Determine o campo elétrico na região .

Duas partículas pontuais, cada uma com massa e carga positiva (que chamaremos de partículas ), estão penduradas por fios de comprimento , em equilíbrio estável, como mostra a primeira Figura 1.1 abaixo.

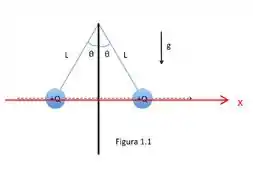
Escolha um sistema de coordenadas apropriado. Em seguida:

1. Calcule a força elétrica (módulo, direção e sentido) exercida pelas duas partículas , uma sobre a outra, em função de , e .
2. Encontre uma equação para o ângulo de equilíbrio em função de , , e . (Você não precisa resolver essa equação!)

Agora, as mesmas duas partículas do caso anterior estão fixadas nas extremidades de uma haste horizontal de comprimento total , por sua vez presa a uma haste vertical, como mostra a Figura 1.2 abaixo. Uma outra partícula, de carga igual a e de massa , pode deslizar ao longo da haste vertical. Sabendo que, na situação da Figura 1.2, a mesma se encontra em equilíbrio estático, sob a ação de seu peso e das forças eletrostáticas exercidas pelas outras duas partículas.



3. Calcule o valor da carga .

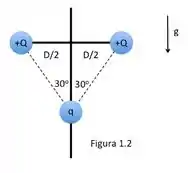
Finalmente, trocamos a partícula de carga e massa por outra de carga e massa . Mais uma vez, a nova partícula atinge o equilíbrio estático, sob a ação de seu peso e das forças eletrostáticas exercidas pelas outras duas partículas.

4. Calcule, nesta nova condição de equilíbrio, a que altura abaixo da haste horizontal a nova partícula () vai se situar.

R com densidade superficial de carga uniforme , e uma barra delgada de comprimento com densidade linear de carga uniforme . Considere o potencial nulo no infinito e use .

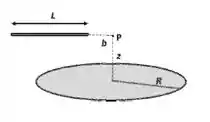
O ponto está sobre o eixo do disco à distância de seu centro e, simultaneamente, sobre o eixo da barra, à distância de sua extremidade mais próxima. (Nos itens () e () você pode escolher sistemas de coordenadas diferentes e convenientes a cada caso.)

1. Considerando apenas o disco, calcule o potencial elétrico em .
2. Considerando apenas a barra, calcule o potencial elétrico em .

Considere, agora, outros dois pontos e do espaço (não mostrados na figura). No ponto , os potenciais do disco e da barra, separadamente, possuem valor e . No ponto , os potenciais valem e . Na presença tanto do disco quanto da barra, uma partícula de massa e carga é abandonada a partir do repouso do ponto e, sob ação exclusivamente das forças elétricas, passa pelo ponto .

3. Calcule a velocidade da partícula ao passar por .