R com densidade superficial de carga uniforme , e uma barra delgada de comprimento com densidade linear de carga uniforme . Considere o potencial nulo no infinito e use .

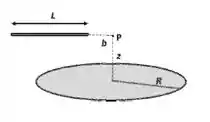
O ponto está sobre o eixo do disco à distância de seu centro e, simultaneamente, sobre o eixo da barra, à distância de sua extremidade mais próxima. (Nos itens () e () você pode escolher sistemas de coordenadas diferentes e convenientes a cada caso.)

1. Considerando apenas o disco, calcule o potencial elétrico em .
2. Considerando apenas a barra, calcule o potencial elétrico em .

Considere, agora, outros dois pontos e do espaço (não mostrados na figura). No ponto , os potenciais do disco e da barra, separadamente, possuem valor e . No ponto , os potenciais valem e . Na presença tanto do disco quanto da barra, uma partícula de massa e carga é abandonada a partir do repouso do ponto e, sob ação exclusivamente das forças elétricas, passa pelo ponto .

3. Calcule a velocidade da partícula ao passar por .

b) Para encontrarmos o potencial que a barra gera em , vamos olhar para a figura abaixo, em que desenhamos a barra isolada, com o sistema de referência mostrado na figura, e o elemento de carga a uma distância do ponto .

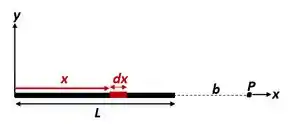
Baseado nisso, o potencial total gerado pela barra é

Quando resolvemos essa integral, vamos obter

c) Como nosso problema se trata de interações eletrostáticas, temos forças conservativas e, portanto, a energia mecânica é conservada. Como a energia mecânica é a soma das energias cinética e potencial, ela terá o mesmo valor nos pontos e S:

Podemos escrever a energia potencial como , e é a soma dos potenciais nos pontos devidos à barra e ao disco nas posições e .

No ponto , o potencial total será

e no ponto , será:

Como a carga parte do repouso no ponto , então:

Portanto, teremos o seguinte

A velocidade da carga ao passar pelo ponto vai ser igual a