Duas partículas pontuais, cada uma com massa e carga positiva (que chamaremos de partículas ), estão penduradas por fios de comprimento , em equilíbrio estável, como mostra a primeira Figura 1.1 abaixo.
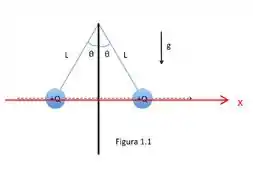
Escolha um sistema de coordenadas apropriado. Em seguida:
- Calcule a força elétrica (módulo, direção e sentido) exercida pelas duas partículas , uma sobre a outra, em função de , e .
- Encontre uma equação para o ângulo de equilíbrio em função de , , e . (Você não precisa resolver essa equação!)
- Calcule o valor da carga .
- Calcule, nesta nova condição de equilíbrio, a que altura abaixo da haste horizontal a nova partícula () vai se situar.
Agora, as mesmas duas partículas do caso anterior estão fixadas nas extremidades de uma haste horizontal de comprimento total , por sua vez presa a uma haste vertical, como mostra a Figura 1.2 abaixo. Uma outra partícula, de carga igual a e de massa , pode deslizar ao longo da haste vertical. Sabendo que, na situação da Figura 1.2, a mesma se encontra em equilíbrio estático, sob a ação de seu peso e das forças eletrostáticas exercidas pelas outras duas partículas.
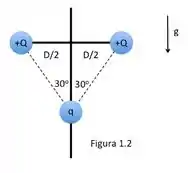
Finalmente, trocamos a partícula de carga e massa por outra de carga e massa . Mais uma vez, a nova partícula atinge o equilíbrio estático, sob a ação de seu peso e das forças eletrostáticas exercidas pelas outras duas partículas.
Passo 1
a) Temos duas cargas positivas, então, a força entre elas será de repulsão e vamos tomar o eixo que mostramos na figura abaixo. A força sobre a carga positiva da direita estará apontando na direção e sentido de , enquanto a força sobre a partícula da esquerda estará apontando para , como está na figura.
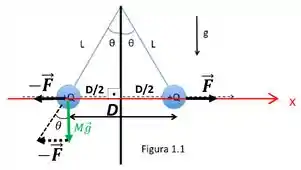
O módulo da força é dado pela lei de Coulomb:
Agora, olhando para o ângulo do triângulo retângulo da figura acima, teremos:
Jogando na expressão para o módulo, o vetor força sobre a partícula da direita será
enquanto que sobre a da esquerda, teremos uma força igual a
sendo que .
Passo 2
b) Olhando para a figura acima e usando que , vemos que a tangente do ângulo fornece o seguinte:
Passo 3
c) No caso deste item, precisamos encontrar qual é o sinal da carga . O problema diz que essa carga está em equilíbrio e que sobre ela atua a força peso apontando para baixo. Isso significa que essa carga deve ser negativa, já que, como mostra a figura abaixo, isso resultaria em uma força na direção vertical que cancela a força peso .
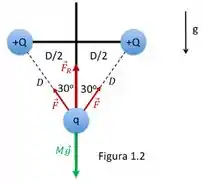
A força resultante devida às cargas estará na vertical e terá módulo igual a
Igualando essa força a
Isso também fornece a seguinte razão
Passo 4
d) Como mostra a equação acima, a razão não muda se alterarmos a carga e a massa da partícula para e , respectivamente. Portanto, a posição de equilíbrio dessa nova carga será a mesma que a do caso anterior, que será, então,