Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força Magnética

Ver Teoria
Exercício 401234567891011121314151617181920212223242526272829303132333435363738394142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Em uma região do espaço existe um campo magnético de magnitude B   =   B o   ẑ (onde ẑ =   k ). Um aro condutor, de resistência constante R , é descrito pela equação no plano x - y   ( t   >   0 ) :

x 2 + y 2 = r 1 2 ,   o n d e   r 1 = r 0 1 + t / τ

onde τ é uma constante com dimensão de tempo. Esse aro se expande com o tempo.

a) Calcule o fluxo magnético no aro como função do tempo.

b) Calcule a f.e.m. no aro e a corrente i ( t ) sobre o mesmo. Justifique se a corrente flui no sentido horário ou anti-horário quando a orientação positiva do aro é dada pelo vetor unitário ẑ (ou seja, o sentido positivo é o anti-horário).

c) Calcule a energia total dissipada no aro entre os instantes t = 0 e t = τ .

Passo 1

Antes de começarmos essa questão, que tal desenharmos esse arco aí?

Bem, de acordo com o enunciado, se trata de um arco condutor no plano x y , basicamente x 2 + y 2 = r 1 2 é uma circunferência de raio r 1 com centro no eixo z ...

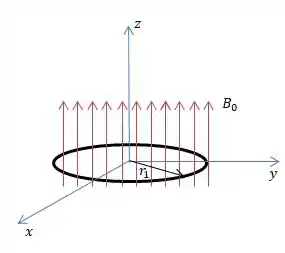
Só que esse aro está inserido nesse campo magnético B   =   B o   ẑ e ele estão se expandindo com o tempo t , já que o raio cresce com o tempo...

r 1 = r 0 1 + t / τ

E à medida que o aro se expande mais campo magnético entra área da região fazendo o fluxo ϕ B aumentar com o tempo. Bem, isso vai fazer gerar uma f e m em cima do aro e, portanto vai também surgir uma corrente elétrica aí devido a Lei de Faraday-Lenz. Mas vamos deixar isso para depois, beleza? Primeiro vamos para a Letra A.

Passo 2

L e t r a   A :

Nesse item aqui é para a gente calcular primeiro o fluxo ϕ B de campo magnético no aro.

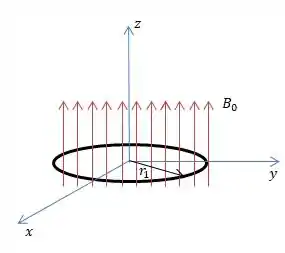
Bem, como o campo magnético é perpendicular à área do aro, o fluxo vai ser simplesmente...

ϕ B = A r e a ⋅ B 0

E a área é conhecida também...

ϕ B = π r 1 2 ⋅ B 0     →

ϕ B = π r 0 1 + t τ 2 ⋅ B 0     →

ϕ B = π r 0 2 1 + t τ 2 B 0

Passo 3

L e t r a   B :

Agora sim é para calcularmos a f e m   ε t induzida e posteriormente a corrente elétrica que surgir. A corrente é mais fácil encontrar porque basta dividir a f e m pela resistência do aro...

i t = ε t R

Por outro lado, a f e m   pode ser obtida pela Lei de Faraday...

ε t = d ϕ B d t = d d t π r 0 2 1 + t τ 2 B 0     →

Tirando as constantes para fora da derivada...

ε t = π r 0 2 B 0   d d t 1 + t τ 2   →

Aplicando a regra da cadeia...

ε t = π r 0 2 B 0   2 1 + t τ     d d t 1 + t τ   →

ε t = π r 0 2 B 0   2 1 + t τ ⋅ 1 τ  

A corrente no aro então vai ser...

i t = ε t R     →

i t = π r 0 2 B 0   2 1 + t τ ⋅ 1 R τ

Agora qual é o sentido dessa corrente?

Passo 4

Observando a figura mais uma vez...

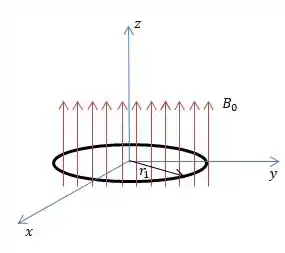
Repare que o fluxo do campo externo B 0 aumenta o que significa que pela Lei de Lenz deverá surgir uma corrente na espira de modo que o campo magnético dessa corrente induzida vá contra esse aumento no fluxo do campo externo.

Ora, se o aro está expandindo, então o fluxo do campo externo B 0 aumenta para cima, então a corrente induzida deve gerar um campo magnético para baixo, e isso só acontece se a corrente induzida girar no sentido horário quando vista de cima .

Passo 5

L e t r a   C :

A energia total dissipada pela corrente em cima dessa espira de resistência R será..

U d i s = ∫ 0 τ R   i 2 t d t  

Então...

U d i s = ∫ 0 τ R   π r 0 2 B 0   2 1 + t τ ⋅ 1 R τ 2 d t       →

U d i s = ∫ 0 τ R   π 2 r 0 4 B 0 2   4 1 + t τ 2 ⋅ 1 R 2 τ 2 d t       →

Tirando todos os elementos constantes dessa integral...

U d i s = 4 π 2 r 0 4 B 0 2 R τ 2 ∫ 0 τ 1 + t τ 2 d t       →

U d i s = 4 π 2 r 0 4 B 0 2 R τ 2 ∫ 0 τ 1 + 2 t τ + t 2 τ 2 d t       →

Integrando...

U d i s = 4 π 2 r 0 4 B 0 2 R τ 2 t + t 2 τ + t 3 3 τ 2 0 τ     →

U d i s = 4 π 2 r 0 4 B 0 2 R τ 2 τ + τ 2 τ + τ 3 3 τ 2     →

U d i s = 4 π 2 r 0 4 B 0 2 R τ 2 τ + τ + 1 3 τ     →

U d i s = 4 π 2 r 0 4 B 0 2 R τ 2 7 τ 3     →

U d i s = 28   π 2 r 0 4 B 0 2 3 R τ

Resposta

Letra A:

ϕ B = π r 0 2 1 + t τ 2 B 0

Letra B:

ε t = π r 0 2 B 0   2 1 + t τ ⋅ 1 τ                     e                   i t = ε t = π r 0 2 B 0   2 1 + t τ ⋅ 1 R τ       ( h o r á r i o )

Letra C:

U d i s = 28   π 2 r 0 4 B 0 2 3 R τ

Exercícios de Livros Relacionados

Em um modelo pré-mecânica quântica para o átomo de hidrogênio, um elétron orbita em torno de um próton a um raio de 5,29 × 10 - 11m . De acordo com este modelo, qual é a magnitude do campo magnético n
Uma barra metálica de massa m desliza em um par de longos trilhos horizontais condutores, paralelos, separados por uma distância L e conectados a um dispositivo que fornece corrente constante I para o
Um próton está se movendo em uma região onde existe um campo magnético uniforme dado por B → = 10 i ^ – 20 j ^ + 30 k ^ m T . No instante t 1 , o próton possui uma velocidade dada por v → = v x i ^ +
Uma partícula alfa se move com uma velocidade v → de módulo 550 m / s em uma região onde existe um campo magnético B → de módulo 0,045 T . (Uma partícula alfa possui uma carga de + 3,2 × 10 - 19 C e u
Um elétron possui uma velocidade inicial de 12,0 j ^ + 15,0 k ^ k m / s e uma aceleração constante de 2,00 × 10 12 m / s 2 i ^ em uma região na qual existem um campo elétrico e um campo magnético, amb