No circuito RLC em série e sem fonte da Figura 1, , e . No instante , a corrente no circuito é , a carga no capacitor é e o capacitor está sendo carregado (isto é, a carga é positiva e aumenta).
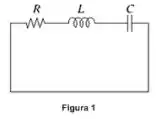
Inicialmente, suponha que o resistor não existe.
(a) Determine a carga máxima no capacitor.
(b) Determine a corrente máxima no circuito.
(c) Se a carga no capacitor é dada por , determine o ângulo de fase .
Em seguida, considere a existência do resistor.
(d) Apresente, justificando, a nova expressão para . Em seguida, apresente um algoritmo (um procedimento detalhado, mas sem realizar as contas) para a determinação dos parâmetros e a partir dos dados do problema (, , , , ).
Passo 1
Bem, para os três primeiro itens, o problema nos pediu que desconsiderássemos a resistência, ou seja, trata-se de um circuito ...
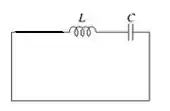
E em um circuito , sabemos que a energia se conserva, isto é, a energia armazenada no início (), é igual à energia armazenada no indutor e no capacitor em qualquer instante de tempo ...
Então a gente vai usar essa belezinha para determinar a solução dos primeiros itens, vamos nessa?
Passo 2
No início, sabemos que tanto o indutor quanto o capacitor estão carregados, já que o indutor possui uma corrente inicial de e o capacitor uma carga .
E de acordo com a teoria, a energia de um indutor e de um capacitor pode ser dada por...
Então, a energia inicial armazenada no circuito é...
Podemos calcular essa energia dada que e , então...
Simplificando ainda mais...
Então a energia inicial armazenada no sistema é...
Passo 3
Então agora vamos determinar a carga máxima no capacitor. Mas como fazer isso a partira da energia?
Ora, sabemos que a energia se conserva...
E há de concordar comigo que a carga vai ser máxima no capacitor quando não tiver nenhuma corrente no indutor! Isso significa que a energia nesse instante vai estar apenas no capacitor...
Então...
Substituindo os valores...
Ou ainda...
Passo 4
Usando o mesmo conceito, podemos usar a corrente máxima que atravessa o indutor...
Substituindo os valores...
Ou ainda...
Passo 5
Ora... Sabemos que a carga no capacitor é dada por...
E foi nos dito que no tempo inicial a carga é . Então...
Logo...
Passo 6
Cara... Agora nós devemos considerar o circuito já com a resistência...
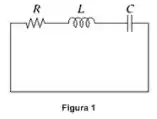
Nesse caso teremos um amortecimento, ou seja, vai circular uma corrente devido a parte , até parar por completo devida a presença do resistor, elemento que dispersa a energia por calor.
O fator de amortecimento de um circuito é dado por ...
E a frequência angular do sistema ...
Ou seja, , o que significa que o amortecimento é suave, ou seja, a corrente vibra até parar por completo. Quando isso acontece num circuito , é porque a carga presente no capacitor possui a seguinte equação...
Onde...
Sendo assim, conhecendo o perfil da carga no capacitor, podemos saber a corrente, no circuito, já que...
Derivando...
E olha que massa, a gente conhece a carga inicial e também conhecemos a corrente inicial , então usando as duas equações e podemos montar o sistema...
Ou ainda...
Repare que esse é um sistema (duas equações e duas incógnitas e ), já que a gente conhece , , e . Então podemos encontrar os valores de e a partir dele que podem não serem os mesmos encontrados, já que aqui temos um sistema amortecido.
Resposta
Letra A:
Letra B:
Letra C:
Letra D: