Um “dimmer” é um dispositivo que permite variar a intensidade luminosa de uma lâmpada. Estes dispositivos são compostos por uma bobina de indutância variável em série com uma lâmpada (Figura 1). A lâmpada é o elemento resistivo do circuito. O valor da indutância da bobina pode assumir qualquer valor entre e .
O circuito da Figura 1 é alimentado por um gerador alternado com uma f.e.m. eficaz e uma frequência angular . Considere que a potência média dissipada pela lâmpada não pode exceder e que a sua resistência elétrica é constante (não varia nem com a temperatura nem com outros fatores).
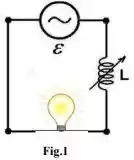
a) Calcule qual deve ser o valor mínimo da indutância no intervalo fornecido para que a potência média dissipada na lâmpada seja máxima . Calcule também o valor da resistência da lâmpada.
b) Calcule qual deve ser o valor da indutância para que a potência média dissipada pela lâmpada seja .
c) Se no lugar do gerador de f.e.m. alternada fosse inserida uma bateria de corrente continua , qual deveria ser o valor da tensão para que, decorrido um tempo muito longo, a potência dissipada na lâmpada fosse de ?
Considere novamente o circuito da Figura 1. Agora a lâmpada é substituída por um resistor e no circuito é inserido em série um capacitor .
d) (0,5) Considerando que a indutância possui o valor máximo calculado no item (b) desenhe o diagrama de fasores do circuito. A corrente que passa no circuito está adiantada ou atrasada em relação à tensão do gerador?
e) (1,0) Variando o valor da indutância L entre os limites permitidos, e , é possível fazer com que o circuito entre em ressonância? No caso de resposta negativa, justifique. No caso de resposta afirmativa, calcule o valor de para que isso aconteça.
Passo 1
POW! Trata-se de um circuito , pois a lâmpada é um elemento Resistivo e temos a presença de um indutor então...
Sabemos que a potência só pode ser dissipada pelo elemento resistivo, no caso a lâmpada. A potência dissipada pode ser dada pela teoria por...
Onde é a corrente eficaz que circula no circuito. Queremos que a potência consumida pela lâmpada seja a máxima possível (), e para isso precisamos que a corrente eficaz seja a máxima possível também. Vamos ver como a gente faz isso?
Passo 2
A corrente eficaz, pode ser dado pela Lei de Ohm...
Onde é a impedância do circuito. Para um circuito no geral essa impedância é dada por...
Mas como se trata de um circuito ...
Então...
Então veja que a gente só consegue uma corrente máxima se for mínimo possível. Como varia de até , podemos dizer que a potência máxima então é atingida se , ou seja ...
Logo...
Como a potência é máxima nesse caso ()...
Essa então é a resistência da lâmpada.
Passo 3
Para resolver esse problema, devemos apenas brincar um pouco com as equações da potência...
E a Lei de Ohm...
Queremos uma potência média de ...
Mas...
Então...
Elevando todo mundo ao quadrado...
E sabendo que os valores de e
Passo 4
POW! Se no lugar da a gente inserisse uma bateria de corrente contínua...
Após um longo período de tempo, independente da indutância , o indutor viraria um curto circuito, isto é, um cabo...

E aí, a potência dissipada na lâmpada seria simplesmente...
Para atingir , sabendo que ...
Ou seja, a bateria deveria ter uma tensão de , ta ligado?
Passo 5
Agora, a gente troca alampada por uma resistência de e insere em série um capacitor
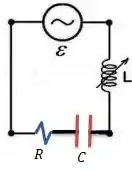
E o problema pede para consideramos . A partir daqui temos que construir o diagrama de fases desse circuito. Para isso, antes de sairmos desenhando o diagrama feito louco, vamos encontrar alguns dados que todo precisa ter:
OBS: Vamos considerar que a corrente do circuito seja e ela é sempre comum a todos os elementos de um circuito série.
- Tensão em cima do resistor: a tensão em cima do resistor ela deve estar em fase com a corrente do circuito então...
- Tensão em cima do indutor ...
- Tensão em cima do capacitor ...
POW! Veja que , o que significa que a corrente deve estar atrasada em relação à tensão da fonte e o ângulo entre e é (ângulo de fase).
Para construir o diagrama de fases, lembre-se de que a tensão do indutor sempre está avante a corrente por enquanto que a tensão do campacitor está sempre atrás por ...
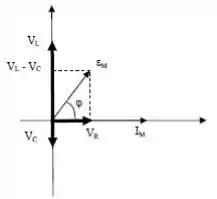
Passo 6
Um sistema entra em ressonância se frequência do sistema () for igual a frequência angular natural de um circuito tal que...
Ou seja...
Como precisaríamos que fosse...
Invertendo e isolando ...
Que é um valor que está entre e , então de fato podemos chegar a ressonância variando .
Resposta
Letra A:
Letra B:
Letra C:
Letra D:
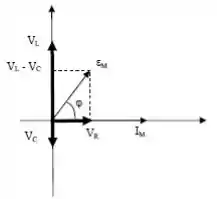
Letra E: