P1 de Física 4 - FIS1061 da PUCRIO - 2016.2

O teorema de Poynting é representado pela equação

a qual descreve o que ocorre com um campo eletromagnético em um volume V do espaço, limitado por uma superfície fechada S de área A, sendo ambos (V e S) regiões simplesmente conexas. O símbolo UEM designa a energia do campo eletromagnético no volume V. O vetor de Poynting é S e o vetor J designa a densidade de corrente elétrica em um ponto no interior do volume V.

(a ) Dê o significado convencional dos termos da equação acima.

Uma fonte luminosa cilíndrica de comprimento L = 0,8 m possui potência P = 100W. A onda luminosa emitida incide sobre uma superfície cilíndrica coaxial com a lâmpada, distante r = 40 m. Em primeira aproximação, determine:

(a) O valor eficaz (rms) do vetor intensidade do campo elétrico .

(b) O valor eficaz (rms) do vetor campo de indução magnética .

Uma onda eletromagnética plana de comprimento de onda 10,0 cm se propaga no vácuo com velocidade no sentido positivo do eixo x. O campo de indução magnética oscila no eixo OZ com valor máximo de 8,00 x Tesla.

(a) Calcule os valores do número de onda k e da frequência angular ω. Escreva a função do vetor campo de indução magnética na forma senoidal em termos dos dados fornecidos. Considere a constante de fase nula.

(b) Determine a função do vetor campo elétrico , sabendo que , onde x designa o produto vetorial e designa o vetor unitário na direção da velocidade da onda (cujo módulo é c).

(c) Encontre a função do vetor de Poynting S(x,t) e a intensidade (I) dessa onda.

Pode-se obter, a partir das equações de Maxwell, as equações que regem os campos

elétrico e magnético de uma onda em um meio condutor. A do campo elétrico é:

Admitindo o vetor intensidade do campo elétrico na forma

como solução da equação acima, obtém-se

evidenciando que o vetor de onda k é complexo.

(d ) Considere . Substitua esse k na função . Observando como fica essa função, escreva o significado de .

Em um dispositivo de interferência a distância entre duas fendas é 0,10 mm. Incide-se sobre o dispositivo uma onda eletromagnética de comprimento de onda λ = 480 nm. A tela de observação está situada a 10,0 m do anteparo das fendas.

(I) Considere o dispositivo com duas fendas somente.

(a) Calcule a distância entre os centros das franjas brilhantes de ordem m = 4 e m = 1 formadas na tela de observação.

(II) Considere o dispositivo com N fendas. A intensidade das franjas brilhantes (máximos) na tela de observação é dada por

Existem dois tipos de máximos. Um é dado pela condição tg δ = 0 e o outro satisfaz a condição tg δ ≠ 0. Designa-se por MÁXIMOS PRINCIPAIS aqueles do tipo que têm maior intensidade que os do outro tipo.

(b ) A partir de uma dessas condições, obtenha a relação d. senθ = mλ com m = 0, 1, 2, 3, . .. para os máximos principais.

(III) Um experimento com anéis de Newton é usado para determinar o raio de curvatura de uma lente. Incide-se luz com comprimento de onda λ = 546 nm perpendicularmente à face plana da lente. Formam-se diversos anéis claros e escuros alternados para um observador situado ao lado da fonte luminosa. O raio do anel claro de ordem m é = 0,162 cm e o raio do anel claro de ordem m + 20 é = 0,368 cm.

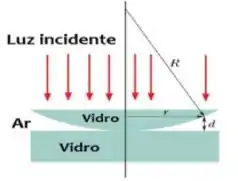
(c ) Calcule o raio R da lente.