P3 de Física 4 da USP - 2012

Considere uma partícula de massa e energia num potencial unidimensional que é nulo na região e infinito para ou .

1. Escreva a função de onda nas regiões e . Justifique.
2. Escreva a equação de Schrödinger independente do tempo na região e as condições de contorno que a função de onda deve satisfazer.
3. Resolva a equação de Schrödinger com as condições de contorno, determinando as funções de onda (não é necessário normalizá-las) e os níveis de energia.

A função de onda normalizada do elétron no estado fundamental do átomo de hidrogênio é dada por

onde é o raio de Bohr e é a distância ao núcleo.

1. Calcule a probabilidade de encontrarmos o elétron, no estado fundamental, dentro de uma esfera de raio centrada no núcleo.
2. Qual é o módulo do momento angular no modelo de Bohr e na mecânica quântica de Schrödinger para o elétron no estado fundamental? Expresse suas respostas em termos de .
3. Se um átomo de hidrogênio estiver no 3º nível excitado (), qual é o nível final atingido após a emissão de um fóton com maior comprimento de onda possível? Explique.

Uma partícula de massa , confinada num poço de potencial como indicado na figura, tem energia total .

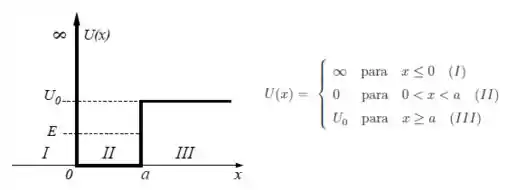
A função de onda da partícula é

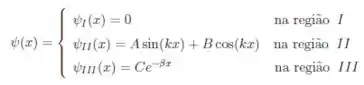
1. Determine a probabilidade da partícula estar na região (), supondo conhecidas as constantes , , , e da função de onda e que ela está normalizada.
2. Determine as constantes e .
3. Escreva as condições de contorno que a função de onda deve satisfazer (não é necessário resolvê-las ).