Origem do Exercício
Uma partícula de massa , confinada num poço de potencial como indicado na figura, tem energia total .
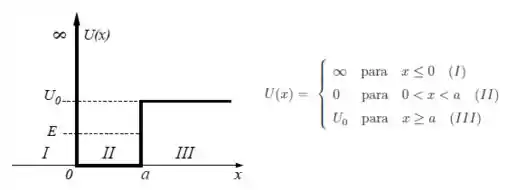
A função de onda da partícula é
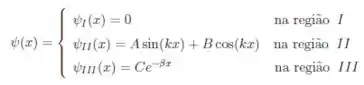
- Determine a probabilidade da partícula estar na região (), supondo conhecidas as constantes , , , e da função de onda e que ela está normalizada.
- Determine as constantes e .
- Escreva as condições de contorno que a função de onda deve satisfazer (não é necessário resolvê-las ).
Passo 1
Letra a)
A probabilidade da partícula estar na região III é dada por:
Passo 2
Letra b)
A equação de Schrödinger na região II é dada por:
Substituindo a função de onda, temos:
Comparando as duas equações, vemos que elas são equivalentes se fizermos:
Passo 3
Para achar , faremos o mesmo para a região III. Para esta,
Que pode ser rearrumada:
Substituindo a função de onda:
As duas equações serão iguais se fizermos:
Passo 4
Letra c)
As condições de contorno necessárias advém da continuidade da função de onda e de suas derivadas quando a função não é nula. Assim:
Resposta
Letra a)
Letra b)
Letra c)
Exercícios de Livros Relacionados
Esboce (a) a função de onda e (b) a função de densidade de probabilidade para o estado n = 5 do potencial finito do poço quadrado
Esboce (a) a função de onda e (b) a função de densidade de probabilidade para o estado n = 4 do potencial finito do poço quadrado
Como sugere a figura 39-8, a densidade de probabilidade na região 0xL do poço de potencial finito da figura 39-7 varia senoidalmente, de acordo com a equação ψ 2 x = B s e n 2 k x , onde B é uma const
Como sugere a figura 39-8, a densidade de probabilidade na região xL do poço de potencial finito da figura 39-7 diminui exponencialmente, de acordo com a equação ψ 2 x = C e - 2 k x , onde C é uma con