P3 de Física 4 da USP - 2018

Considere a seguinte função de onda do elétron no átomo de hidrogênio dada por:

Onde é o raio de Bohr e é uma constante real.

(a) Calcule a distância, medida a partir do centro do núcleo, onde a probabilidade radial de encontrar o elétron é máxima.

(b) Calcule a constante C e o valor médio de r nesse estado.

(c) Quais são os números quânticos associados ao estado do elétron correspondente à função de onda acima? Obtenha o módulo do momento angular orbital L.

Uma partícula de massa m, confinada num poço de potencial como indicado na figura, tem energia total

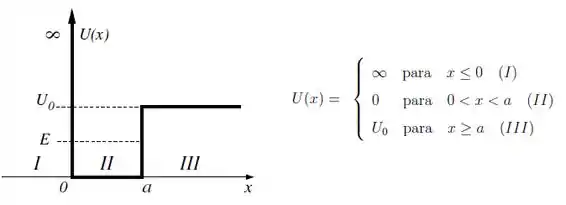
(a) Escreva a solução geral da equação de Schrödinger independente do tempo em termos dos parâmetros do problema. Justificar as respostas através da análise da equação de Schrödinger. Não é necessário encontrar o valor das constantes arbitrárias não nulas.

(b) Escreva as condições de contorno que a função de onda deve satisfazer (não é necessário resolvê-las).

(c) Determine a probabilidade de a partícula estar na região III , em termos das constantes obtidas no item (a).

Considere um elétron que esteja confinado dentro de um poço de potencial unidimensional, com altura infinita e largura d.

(a) Escreva a equação de Schrödinger independente do tempo para este elétron na região (dentro do poço).

(b) Obtenha as soluções normalizadas do problema acima e as correspondentes energias permitidas para o elétron na região

(c) Considere agora que o elétron se encontra no estado quântico descrito pela função de onda , sendo A a constante de normalização obtida no item (b). Determine o comprimento de onda de de Broglie e o momento linear associado à este estado.

(d) Para o mesmo estado do item (c), determine a probabilidade de encontrar o elétron entre e