P3 de Física 4 da USP - 2019

. PARTE

Um átomo de hidrogênio sofre uma transição eletrônica do estado para o estado , emitindo um fóton. A transição transcorre num intervalo de tempo , denominado “tempo de vida” do estado . Admitindo que a incerteza na posição do fóton seja igual ao comprimento do pulso de luz associado ao fóton emitido, estime a incerteza no momento linear do fóton.

. PARTE 2

Um elétron encontra-se num poço de potencial unidimensional com barreiras infinitas, situado entre . No instante , a função de onda deste elétron é dada por , sendo uma constante real.

Encontre a derivada na posição no instante . Expresse sua resposta em termos de e das constantes universais.

Justique se o estado acima é estacionário.

A função de onda do elétron no átomo de hidrogênio, no estado , é dada por

onde é o raio de Bohr e é uma constante real.

Determine a região do espaço em torno do próton onde a energia deste elétron, na descrição da mecânica quântica, é menor do que a energia potencial do elétron, na descrição da mecânica clássica. Apresente a resposta em termos do raio de Bohr .

Use a condição de normalização para determinar o valor de .

Para este estado, escreva a expressão da distribuição de probabilidade radial (densidade de probabilidade radial). Calcule o valor de para o qual ela é máxima.

Calcule o valor numérico da probabilidade de encontrar o elétron a uma distância maior do que . Utilize as estimativas para potências de : , , , .

. Uma partícula de massa se move em uma dimensão na presença de um poço de potencial

de profundidade e largura conforme a figura abaixo. A partícula se encontra num estado estacionário de energia .

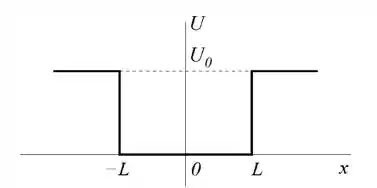
(a) Escreva a equação de Schrödinger independente do tempo desta partícula para e sua solução geral.

(b) Escreva a equação de Schrödinger independente do tempo desta partícula para e e sua solução geral. Qual solução é fisicamente aceitável?

(c) Encontre as condições de contorno que as constantes arbitrárias introduzidas nos itens e devem satisfazer (não é necessário resolver o sistema).

(d) Calcule a probabilidade de encontrar a partícula na região como

função dessas constantes.