P3 de Física 4 da USP - 2015

Uma partícula de massa se move em uma dimensão na presença de um “poço de potencial” de profundidade e largura conforme a figura . A partícula se encontra num estado estacionário de energia .

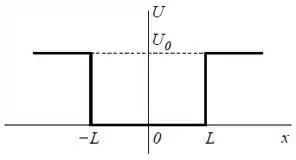
1. A densidade de probabilidade de se encontrar a partícula em uma das regiões fora do poço é , onde e são constantes positivas. Explicite a região fora do poço na qual é aceitável esta densidade e explique o porquê. Calcule a probabilidade de encontrar a partícula nesta região (suponha e conhecidos).
2. Calcule a constante para que a função de onda associada à densidade de probabilidade satisfaça a equação de Schrödinger na região apropriada.
3. Escreva a equação de Schrödinger para a região e determine a solução geral desta equação.

Nesta questão denotamos por os estados do átomo de hidrogênio sem levar em conta o spin do elétron, onde , e são respectivamente os números quânticos principal, orbital e magnético. Os números quânticos magnéticos foram determinados com respeito a um campo magnético com componente somente na direção .

1. A função de onda do estado fundamental do átomo de hidrogênio é

onde é o raio de Bohr. Calcule o valor da constante de normalização.

2. Um elétron está no estado . Considere a energia e o momento angular orbital e seu módulo . Quais são os valores de , e ?
3. Considere agora um átomo com muitos elétrons na aproximação onde se despreza a interação entre os elétrons. Neste caso, a função de onda de cada elétron é semelhante à do hidrogênio e possui os mesmos números quânticos. Levando em conta o número quântico de spin, determine o número máximo de elétrons que possuem o número quântico principal igual a .

Uma partícula de massa e energia que se move em uma dimensão possui energia potencial que varia com a posição como mostra a figura.

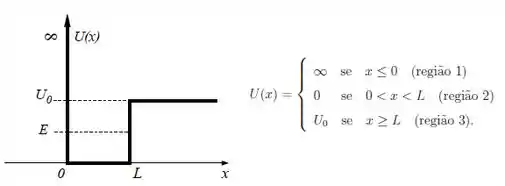
A função de onda estacionária para esta partícula pode ser obtida separadamente em cada região do espaço, sendo assim especificada por:

1. Para o caso , escreva a solução geral para , e , expressando-as, quando for o caso, em termos de combinações lineares das funções e , onde as constantes e são ambas reais e positivas.
2. Calcule os valores de e como função de , e constantes do problema.
3. Que condições de contorno as soluções , e devem satisfazer nos pontos e .

Uma partícula de massa executa oscilações em uma reta em torno de sua posição de equilíbrio em , sujeita a um potencial harmônico dado por , com e uma constante. A função de onda do estado fundamental da partícula é

onde e são constantes positivas.

1. Calcule e a energia do estado fundamental do oscilador, em termos dos parâmetros dados: , , e .
2. Calcule a constante .
3. Qual é a probabilidade de encontrar a partícula na região .