Uma partícula de massa se move em uma dimensão na presença de um “poço de potencial” de profundidade e largura conforme a figura . A partícula se encontra num estado estacionário de energia .
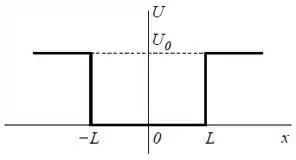
- A densidade de probabilidade de se encontrar a partícula em uma das regiões fora do poço é , onde e são constantes positivas. Explicite a região fora do poço na qual é aceitável esta densidade e explique o porquê. Calcule a probabilidade de encontrar a partícula nesta região (suponha e conhecidos).
- Calcule a constante para que a função de onda associada à densidade de probabilidade satisfaça a equação de Schrödinger na região apropriada.
- Escreva a equação de Schrödinger para a região e determine a solução geral desta equação.
Passo 1
Letra a)
A densidade da probabilidade tem que ser tal que ela seja possível de ser normalizada.
Para isso, a integral dela em todas as regiões não pode ser infinita.
Quando vamos andando no sentido negativo do eixo , essa função vai crescendo cada vez mais, sendo que quando , essa densidade de probabilidade tende ao infinito:
Logo, essa densidade não pode descrever a partícula para .
Mas ela pode descrever a partícula na região , pois neste caso:
E podemos normalizar a função!
Passo 2
Agora vamos calcular a probabilidade da partícula se encontrar em . Lembrando que é a densidade de probabilidade, temos:
Passo 3
Letra b)
Sabemos que
Porém, é a função de onda que aparece na equação de Schrödinger. Então, tirando a raíz quadrada:
A equação de Schrödinger nessa região é dada por
Pois a energia potencial é . Rearrumando:
Substituindo nossa função de onda:
O que dá:
Ou seja:
Passo 4
Letra c)
Nesta região, a energia potencial é zero, e a equação de Schrödinger fica:
Agora vamos ajeitá-la de forma que saibamos resolver.
Definindo , temos:
Cuja solução é uma combinação de senos e cossenos (ou de exponenciais complexas)
Resposta
Letra a)
A região é .
Letra b)
Letra c)