Uma partícula de massa m, confinada num poço de potencial como indicado na figura, tem energia total

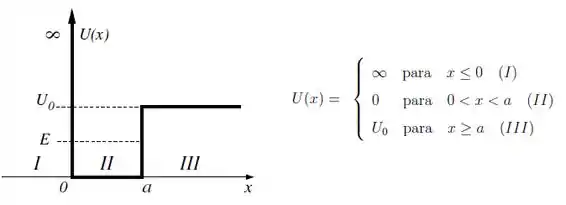
(a) Escreva a solução geral da equação de Schrödinger independente do tempo em termos dos parâmetros do problema. Justificar as respostas através da análise da equação de Schrödinger. Não é necessário encontrar o valor das constantes arbitrárias não nulas.

(b) Escreva as condições de contorno que a função de onda deve satisfazer (não é necessário resolvê-las).

(c) Determine a probabilidade de a partícula estar na região III , em termos das constantes obtidas no item (a).

(a) Lembrando que a equação de Schrödinger é dada por:

Vamos resolvê-la para cada região dada no problema, começando pela região I, que corresponde a

Rearranjando os termos na equação:

Fazendo

A solução dessa equação é:

onde

Isso é porque temos uma derivada segunda de uma função igual a uma constante vezes a própria função, e isso acontece para a função exponencial.

Mas na região I, temos que

Então, fazendo e

Portanto, na região I, a função de onda é:

Na região II, e a equação de Schrödinger fica:

Agora temos uma função cuja derivada segunda é uma menos uma constante vezes a própria função.

Isso ocorre para as funções seno e cosseno, então as duas são possíveis respostas.

Então, como uma combinação linear de soluções de uma equação diferencial também é solução dessa equação, uma solução possível vai ser:

Onde

A questão disse que a gente não precisa determinar A e B, então vamos dizer que na região II a função de onda é:

Por último, pra região III a equação é:

Fazendo

A solução dessa equação é:

onde

Isso é porque de novo temos uma derivada segunda de uma função igual a uma constante vezes a própria função, e isso acontece para a função exponencial.

E essa é a função de onda na região III.