Um corpo de massa parte do repouso no ponto , situado a uma altura sobre uma rampa curva e com atrito desprezível. Admita a energia potencial gravitacional como sendo nula em . O corpo chega ao final da rampa em com velocidade , onde se inicia um trecho horizontal com comprimento . Neste trecho , o coeficiente de atrito cinético entre o corpo e a superfície cresce linearmente com a posição , tal que . Após o ponto o corpo choca-se com uma mola ideal de constante elástica e a comprime uma distância até parar. Durante a compressão da mola, o coeficiente de atrito cinético entre o corpo e a superfície é constante e vale . Utilize considerações de trabalho e energia para responder as perguntas abaixo.

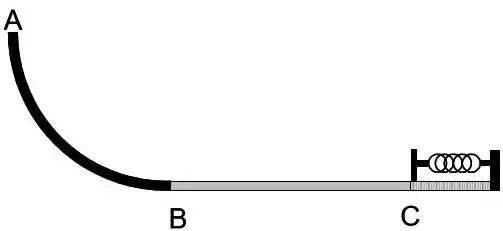
a) Calcule o valor da energia potencial gravitacional do corpo em .

b) Esboce o gráfico do módulo da força de atrito cinético versus a distância percorrida pelo corpo no trecho e calcule o módulo da velocidade que o corpo possui ao atingir a mola em .

c) Usando o Teorema do trabalho-energia cinética, calcule a compressão sofrida pela mola em centímetros.

(b)

Temos que a força de atrito é dada por:

Mas,

E

Logo,

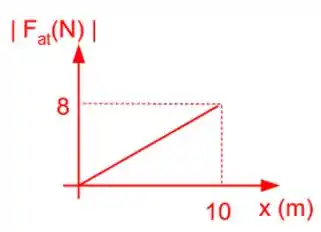
Então, como a força de atrito cresce linearmente com a distância, o gráfico será uma reta:

𝐷𝑒𝑠𝑡𝑎 𝑓𝑜𝑟𝑚𝑎, 𝑐𝑜𝑚𝑜 𝑎𝑡𝑢𝑎𝑚 𝑓𝑜𝑟ç𝑎���� 𝑛ã𝑜 −𝑐𝑜𝑛𝑠𝑒𝑟𝑣𝑎𝑡𝑖𝑣𝑎𝑠 𝑠𝑜𝑏𝑟𝑒 𝑜 𝑠𝑖𝑠𝑡𝑒𝑚𝑎, pelo teorema trabalho-energia:

Entretanto como a plataforma está nivelada entre os pontos e :

Logo:

Para encontrar o 𝑡𝑟𝑎𝑏𝑎𝑙ℎ𝑜 𝑑a força de 𝑎𝑡𝑟𝑖𝑡𝑜, basta calcular a á𝑟𝑒𝑎 𝑑𝑜 𝑔𝑟á𝑓𝑖𝑐𝑜:

Como a força de atrito é contrária a trajetória, o trabalho é negativo. Então:

Substituindo na equação:

(c)

O teorema nos diz que o trabalho da força resultante é igual à variação da energia cinética:

Substituindo os dados do problema:

Logo: