P3 de Física B - FIS1026 da PUCRIO - 2012.2

Seja um corpo rígido composto de uma esfera maciça de massa e raio , uma esfera oca de massa e raio , e uma barra fina de massa e comprimento . Este corpo está sobre uma mesa horizontal e pode girar em torno de um eix vertical fixo que passa no centro da barra, indicado pelo ponto na figura abaixo. Não há atrito com a mesa ou com o eixo de rotação.

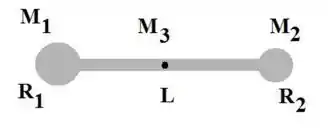
Calcule o momento de inércia deste corpo em relação ao eixo indicado.

Sejam duas forças agindo no centro de cada esfera, como mostrado abaixo. Os módulos das forças aplicadas são e . Encontre o módulo da aceleração angular e o sentido da rotação resultante (horário ou anti-horário).

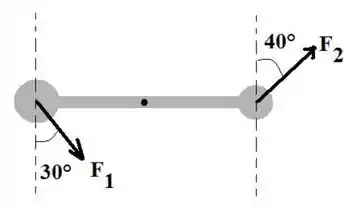
Agora, duas forças agem nas posições indicadas: a força a uma distância L/4 do centro da barra e a força no centro da esfera oca. Os módulos das forças aplicadas são e . Calcule o ângulo necessário para que o corpo não apresente movimento rotacional.

Dois astronautas, cada um tendo massa , estão ligados por uma corda de comprimento , com massa desprezível. Eles se encontram isolados no espaço, orbitando ao redor do centro de massa comum com velocidades escalares , tangenciais à corda, no sentido

mostrado na figura. Modele os astronautas como partículas.

Encontre o módulo do momento angular do sistema em relação ao centro de massa.

Os astronautas começam a puxar a corda simultaneamente de tal forma que, ao final, reduzem sua distância para . Nesta nova configuração, determine o período de rotação dos dois em relação ao centro de massa comum.

Calcule o trabalho total realizado pelos astronautas ao recolher a corda.

A figura a seguir mostra um dispositivo utilizado para puxar uma esfera oca de raio e massa rolando sem deslizar ao longo de um plano com inclinação em relação à horizontal. A esfera é puxada da base do plano inclinado a partir do repouso por uma roldana (disco sólido) de raio e massa pela aplicação de uma força constante na direção tangente à posição de uma manivela (comprimento e massa desprezível) fixada em um eixo que passa no centro de massa da roldana, conforme mostra a vista frontal do dispositivo. Adote , despreze os efeitos de atrito no eixo da roldana e considere o fio ideal.

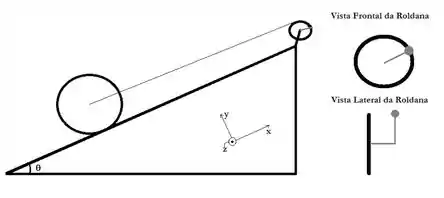
A força é tal que suspende a esfera oca ao longo da rampa com uma aceleração de centro

de massa constante .

Determine a energia cinética da esfera oca dois segundos após o início do movimento.

Determine o vetor momento angular final da esfera oca, em relação ao seu centro de massa, dois segundos após o início do movimento.

Faça o diagrama do corpo livre para a esfera oca e para a roldana e escreva as equações que regem os movimentos destes corpos.

Obtenha o módulo da força aplicada à manivela.