Seja um corpo rígido composto de uma esfera maciça de massa e raio , uma esfera oca de massa e raio , e uma barra fina de massa e comprimento . Este corpo está sobre uma mesa horizontal e pode girar em torno de um eix vertical fixo que passa no centro da barra, indicado pelo ponto na figura abaixo. Não há atrito com a mesa ou com o eixo de rotação.
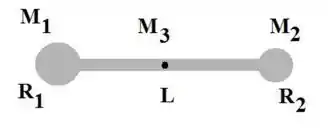
Calcule o momento de inércia deste corpo em relação ao eixo indicado.
Sejam duas forças agindo no centro de cada esfera, como mostrado abaixo. Os módulos das forças aplicadas são e . Encontre o módulo da aceleração angular e o sentido da rotação resultante (horário ou anti-horário).
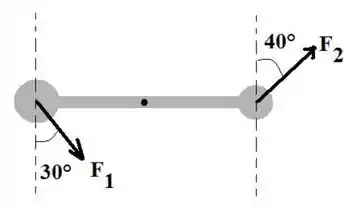
Agora, duas forças agem nas posições indicadas: a força a uma distância L/4 do centro da barra e a força no centro da esfera oca. Os módulos das forças aplicadas são e . Calcule o ângulo necessário para que o corpo não apresente movimento rotacional.
Passo 1
Para calcular o momento de inércia do corpo, podemos calcular cada componente separadamente:
Considerando o eixo dado, podemos calcular o momento de inércia de cada esfera com o teorema dos eixos paralelos! Tá ligado?
Agora é só substituir os valores!
Passo 2
Agora vamos calcular o momento de inércia da barra, como ela gira em torno de seu próprio centro de massa, temos:
substituindo os valor, temos:
Passo 3
Vamos para o último componente, a esfera oca! Para calcular seu momento de inércia, também iremos utilizar o teorema dos eixos paralelos, mão na massa!
Substituindo os valores, temos:
Passo 4
Agora é somar todos os componentes!
Passo 5
Para encontrar o módulo da aceleração, assim como o sentido da rotação, iremos recorrer à segunda Lei de Newton para rotações! Lembra!?
No caso do sistema apresentado, temos:
Pela regra da mão direita, podemos determinar que ambos os torques são perpendiculares ao plano de rotação, e por isso que podemos somar os módulos dos torques!
Agora podemos substituir os valor e achar o módulo da aceleração angular, ainda bem que já calculamos o momento de inércia no item !
Quando usamos a regra da mão direita para determinar a direção e o sentido do torque, estávamos determinando também, o sentido da rotação. Ou seja a rotação se dá no sentido anti-horário.
Passo 6
Para que o corpo não apresente movimento rotacional, o torque resultante deve ser zero, não é mesmo?!
Para o sistema mostrado, fica:
Opaaa....Por que agora os torques não estão sendo somado?! Calma! Se você usar a regra da mão direita vai ver que apesar de teram a mesma direção, eles possuem sentidos opostos. Ahhh ta!!! Continuando...
Isolando , temos:
Resposta