P3 de Física B - FIS1026 da PUCRIO - 2018.1

Considere um carretel de raio externo , massa e momento de inércia em relação ao centro de massa . Ele está em repouso quando uma corda enrolada no cilindro interno de raio é puxada com uma força de tração horizontal constante . O carretel passa a rolar sem deslizar no sentido horário (para a direita) em um plano horizontal com coeficiente de atrito estático . As forças na direção horizontal, atrito e tração, agindo no carretel estão ilustradas na figura.

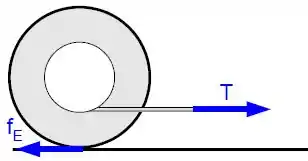
a) Escreva as equações de movimento que descrevem a dinâmica do carretel como translação do centro de massa e rotação em torno do centro de massa.

b) Use as equações do item anterior para obter o modulo da aceleração angular α em relação ao centro de massa do carretel.

c) Qual é o valor máximo da tração para o rolamento sem deslizamento.

Considere um sistema composto por um cilindro de massa e raio , uma haste de massa e comprimento e dois discos de massa . Os discos estão encostados no cilindro, presos por um freio, como ilustra a figura. Um torque externo coloca o sistema em rotação em torno do eixo-y no sentido horário sendo desligado quando a velocidade angular é alcançada. Neste instante o freio que prende os discos é retirado e os discos deslizam pela haste até as suas extremidades.

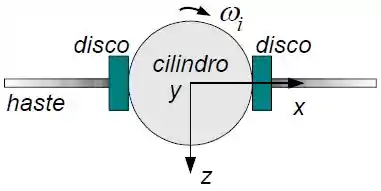
a) Encontre a nova velocidade angular do sistema quando os discos chegarem nas extremidades da haste. Considere os discos como massas pontuais.

Dados: sendo:

;

;

;

;

Um objeto de massa desliza na direção do eixo-x positivo em uma superfície com coeficiente de atrito cinético . O objeto tem uma velocidade quando colide de forma perfeitamente inelástica com uma mola quando ela está no seu ponto de equilíbrio (relaxada). A mola tem uma constante elástica . Durante a compressão da mola o atrito é desprezível. O objeto para momentaneamente, depois de comprimir a mola uma distância . O objeto é então forçado pela mola a se mover na direção do eixo-x negativo junto com a mola passando de novo pelo ponto de equilíbrio até parar momentaneamente a uma distância deste ponto. Considere o objeto como uma massa pontual. Utilize conservação de energia nas respostas abaixo. Justifique seus cálculos.

Dados:

a) Calcule o trabalho sobre o objeto desde o momento em que ele encosta na mola até parar momentaneamente.

b) Determine a distância d que a mola foi comprimida até parar momentaneamente.

c) Determine a velocidade quando o objeto passa pela posição de equilíbrio na volta, isto é se movendo na direção do eixo-x negativo.

d) Lembre que na volta a mola fica presa no objeto. Determine a distância D que a mola foi distendida até parar momentaneamente.

O objeto ilustrado ao lado é composto por um cilindro de raio , uma haste rígida e dois discos afastados do eixo de rotação. O objeto tem momento de inércia . Ao longo do perímetro do cilindro está enrolada uma corda inextensível de massa desprezível. Outra parte desta corda está enrolada em uma roldana de raio e momento de inércia . Na extremidade da corda está uma pequeno cubo de massa , distante de um suporte. Não há deslizamento na corda. Inicialmente o sistema é mantido em repouso através de um freio. No instante o freio é retirado e o sistema inicia seu movimento. Utilize para a aceleração da gravidade.

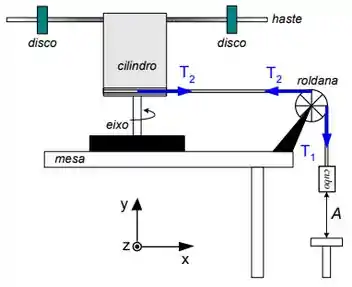
(d) Determine a energia cinética adquirida pelo sistema desde até quando o cubo está prestes a encostar no suporte. Despreze atritos.

O objeto ilustrado ao lado é composto por um cilindro de raio , uma haste rígida e dois discos afastados do eixo de rotação. O objeto tem momento de inércia . Ao longo do perímetro do cilindro está enrolada uma corda inextensível de massa desprezível. Outra parte desta corda está enrolada em uma roldana de raio e momento de inércia . Na extremidade da corda está uma pequeno cubo de massa , distante de um suporte. Não há deslizamento na corda. Inicialmente o sistema é mantido em repouso através de um freio. No instante o freio é retirado e o sistema inicia seu movimento. Utilize para a aceleração da gravidade.

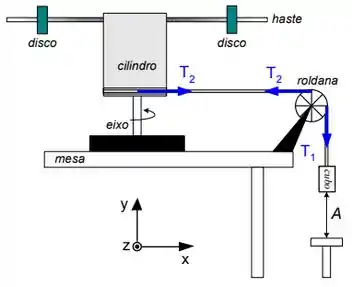
b) Determine a razão entre os módulos das acelerações angulares da roldana e do objeto .

c) Determine o módulo da aceleração linear com que o cubo cai em função dos parâmetros dados.

O objeto ilustrado ao lado é composto por um cilindro de raio , uma haste rígida e dois discos afastados do eixo de rotação. O objeto tem momento de inércia . Ao longo do perímetro do cilindro está enrolada uma corda inextensível de massa desprezível. Outra parte desta corda está enrolada em uma roldana de raio e momento de inércia . Na extremidade da corda está uma pequeno cubo de massa , distante de um suporte. Não há deslizamento na corda. Inicialmente o sistema é mantido em repouso através de um freio. No instante o freio é retirado e o sistema inicia seu movimento. Utilize para a aceleração da gravidade.

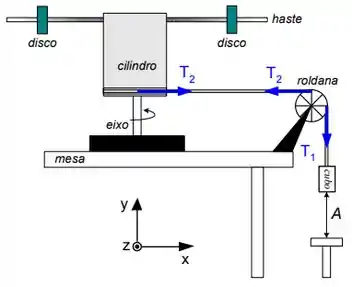
a) Em função das forças indicadas na ilustração, escreva os torques que agem na roldana e no objeto no instante .