A figura a seguir mostra um dispositivo utilizado para puxar uma esfera oca de raio e massa rolando sem deslizar ao longo de um plano com inclinação em relação à horizontal. A esfera é puxada da base do plano inclinado a partir do repouso por uma roldana (disco sólido) de raio e massa pela aplicação de uma força constante na direção tangente à posição de uma manivela (comprimento e massa desprezível) fixada em um eixo que passa no centro de massa da roldana, conforme mostra a vista frontal do dispositivo. Adote , despreze os efeitos de atrito no eixo da roldana e considere o fio ideal.
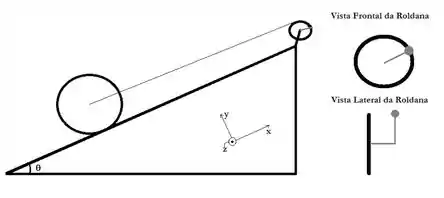
A força é tal que suspende a esfera oca ao longo da rampa com uma aceleração de centro
de massa constante .
Determine a energia cinética da esfera oca dois segundos após o início do movimento.
Determine o vetor momento angular final da esfera oca, em relação ao seu centro de massa, dois segundos após o início do movimento.
Faça o diagrama do corpo livre para a esfera oca e para a roldana e escreva as equações que regem os movimentos destes corpos.
Obtenha o módulo da força aplicada à manivela.
Passo 1
A energia cinética da esfera que está rolando pode ser dividida em energia cinética de translação e de rotação, se liga!
Antes de partir para a substituição, temos que determinar o momento de inércia e a velocidade do centro de massa para !
Passo 2
Para achar a velocidade, nada melhor do que a boa e velha cinemática!
ou seja:
Vamos agora achar o momento de inércia!
Passo 3
Agora que temos todos os valores, podemos achar a energia cinética!
Calma, o não saiu da cartola! É só lembrar que !
Passo 4
Para determinar o vetor momento angular para , devemos lembrar de sua definição, . Como a gente ja calculou o momento de inércia e a velocidade angular no item , fica bem mais fácil!
A intensidade do momento angular é dada por
Já o vetor do momento angular é dado por
De onde surgiu essa direção e sentido?! Como a gente sabe que a rotação se dá no sentido horário, pois a esfera está subindo a rampa, e pela regra da mão direita, a velocidade angular da esfera aponta para dentro da página!
Passo 5
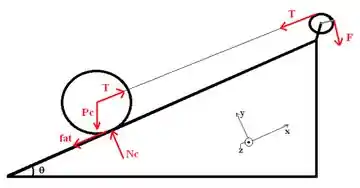
O movimento da Roldana é apenas rotacional, portanto, vamos começar por ela!
Pela segunda Lei de Newton para rotações, temos:
Ou seja:
simplificando:
Lembrando, que como o rolamento é suave, podemos usar !
Passo 6
Agora vamos para as equações que regem o movimento da esfera. Lembrando que agora temos movimento rotacional e translacional, por isso vamos começar com o rotacional!
Simplificando:
Agora vamos para o movimento translacional! Como não existe movimento em , podemos partir direto para a componente !
Em , temos:
Só para confirmar, em , temos:
Passo 7
Para determinar o módulo da força , vamos usar as equações obtidas no item c!
Somando as três equações, isso tudo para poder cancelar os termos desconhecidos, temos:
Isolando a força e substituindo os valores, temos:
Resposta