P3 de Física B - FIS1026 da PUCRIO - 2013.2

Um ioiô com massa e com raio do eixo possui momento de inércia de . Sua corda tem de comprimento, é inextensível e tem massa desprezível. No momento em que é lançado verticalmente para baixo, o ioiô tem somente velocidade de translação . Assuma que não há deslizamento entre a corda e o eixo do ioiô.

Escreva as equações de movimento do ioiô sob sua forma literal.

Determine o valor da aceleração do centro de massa do ioiô durante seu moviemento

Determine a energia cinética total do ioiô no instante em que ele chega 60 cm abaixo do ponto da onde foi lançado.

Determine o valor da energia cinética relacionada ao movimento de rotação neste instante.

O caminhão ilustrado abaixo, está com sua lança esticada desde seu eixo até a sua ponta . Sua inclinação é de em relação à horizontal. A massa da lança é e para simplificar os cálculos considere-a uniformemente distribuída. O caminhão está estacionado, com a lança sustentando uma viga de aço de de comprimento e massa , que se encontra na posição horizontal. De forma a manter tudo em equilíbrio estático, um braço hidráulico no topo da cabine de controle, inclinado de em relação à horizontal, atua com uma força no centro de massa da lança . Despreze o atrito da lança com o eixo e as masas dos cabos e do gancho.

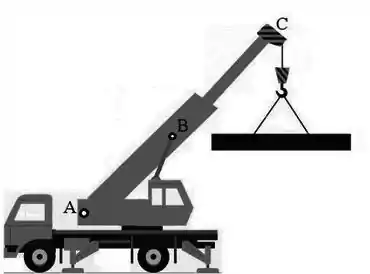
Utilize: ; ; ; .

Determine o vetor torque em relação ao eixo exercido pelo braço hidráulico sobre a lança.

Determine o vetor força que atua sobre a extremidade da lança presa ao eixo

Suponha agora que em determinado instante, o braço hidráulico pare de atuar, calcule para este instante o módulo da aceleração angular da lança.

A figura mostra uma montagem de laboratório utilizada para experiências de momento angular. Ela é composta por 3 corpos: i) uma haste fina de massa e comprimento articulada por um eixo sem atrito (localizado no ponto P) distante de uma de suas extremidades; ii) uma pequena esfera sólida de massa , presa à extremidade mais próxima ao eixo da haste e iii) um aro de raio e massa preso à outra extremidade. A montagem está girando no plano horizontal com velocidade angular (no sentido horário), quando sofre uma colisão ao se encontrar na posição à acima do eixo com uma esfera sólida de massa que se move com velocidade . A esfera fica presa no aro.

Considere as esferas como pontuais. Utilize: ; .

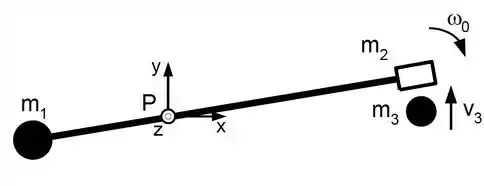
Calcule o momento de inérica de cada componente da montagem em torno do ponto P, formado pela haste fina, esfera de massa e aro.

Calcule o vetor momento angular total do sistema imediatamente antes da colisão (. Responda se haverá ou não conservação do momento angular do conjunto durante a colisão, justificando cuidadosamente.

Calcule o módulo da velocidade angular imediatamente após a colisão e informe também o sentido da rotação do conjunto.